
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 210 Атанасян — Подробные Ответы
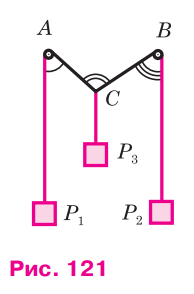
Два тела Р1 и Р2 подвешены на концах нити, перекинутой через блоки A и B (рис. 121).
Третье тело Р3 подвешено к той же нити в точке С и уравновешивает тела Р1 и Р2.
(При этом AP1 || BP2 || CP3.) Докажите, что ∠ACB = ∠CAP1 + ∠CBP2.
Доказательство:
1. Так как AP1 || BP2 || CP3, то углы ∠CAP1 и ∠CBP2 являются углами, образованными секущими с параллельными прямыми. Эти углы связаны с углом ∠ACB через свойства треугольников.
2. Угол ∠ACB является внешним углом треугольников ACP1 и BCP2.
3. Согласно свойству внешнего угла треугольника, внешний угол равен сумме двух несмежных внутренних углов.
4. Следовательно, угол ∠ACB равен сумме углов ∠CAP1 и ∠CBP2.
Дано: Тела Р1 и Р2 подвешены на концах нити, перекинутой через блоки A и B. Тело Р3 подвешено к той же нити в точке С и уравновешивает тела Р1 и Р2. При этом AP1 || BP2 || CP3. Необходимо доказать, что угол ∠ACB равен сумме углов ∠CAP1 и ∠CBP2.
Рассмотрим решение задачи по шагам:
1. Рассмотрим треугольник ACB. В этом треугольнике угол ∠ACB является внешним углом для двух треугольников ACP1 и BCP2. Нам нужно доказать, что ∠ACB = ∠CAP1 + ∠CBP2.
2. По условию задачи, прямые AP1, BP2 и CP3 параллельны. Это означает, что углы, образованные секущими AC и BC с этими параллельными прямыми, связаны между собой.
3. Рассмотрим треугольник ACP1. В этом треугольнике угол ∠CAP1 является внутренним углом, а угол ∠ACP1 является смежным углом к углу ∠ACB. Аналогично, в треугольнике BCP2 угол ∠CBP2 является внутренним углом, а угол ∠BCP2 также является смежным углом к углу ∠ACB.
4. Согласно свойству внешнего угла треугольника, внешний угол равен сумме двух несмежных внутренних углов. Применим это свойство к треугольникам ACP1 и BCP2:
— Для треугольника ACP1 внешний угол ∠ACB равен сумме углов ∠CAP1 и ∠ACP1.
— Для треугольника BCP2 внешний угол ∠ACB равен сумме углов ∠CBP2 и ∠BCP2.
5. Учитывая, что углы ∠ACP1 и ∠BCP2 являются смежными с углом ∠ACB и дополняют его до 180 градусов, их влияние на сумму углов исключается. Остается только сумма углов ∠CAP1 и ∠CBP2.
6. Таким образом, угол ∠ACB равен сумме углов ∠CAP1 и ∠CBP2, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!