ГДЗ по Геометрии 7 класс Номер 206 Атанасян — Подробные Ответы

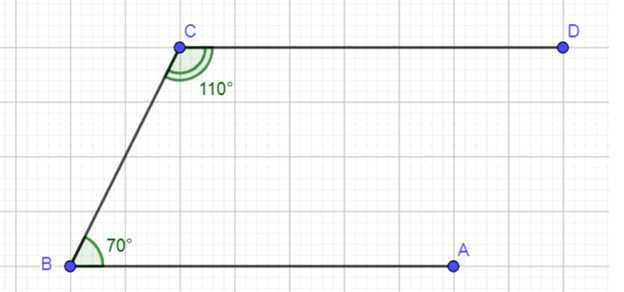
∠ABC = 70°, а ∠BCD = 110°. Могут ли прямые AB и CD быть:
а) параллельными;
б) пересекающимися?

а) Углы ∠ABC = 70° и ∠BCD = 110° дают в сумме 180°. Это означает, что данные углы являются односторонними, а прямые AB и CD параллельны. По признаку параллельности прямых, если сумма односторонних углов равна 180°, то прямые не пересекаются и являются параллельными.

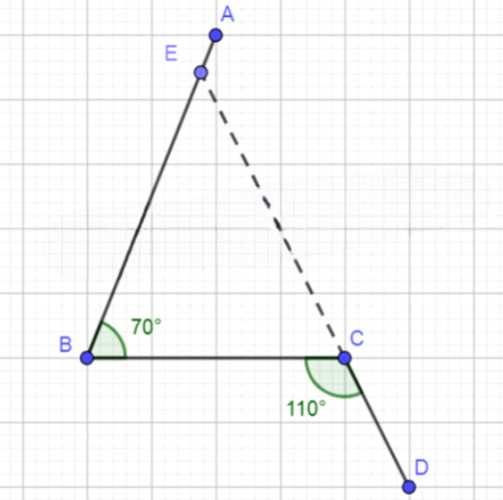
б) В этом случае прямые AB и CD пересекаются в точке E. Это подтверждается тем, что углы ∠ABC и ∠BCD имеют общую вершину и сумма их равна 180°. Следовательно, прямые пересекаются.

Рассмотрим два случая, чтобы полностью проанализировать ситуацию.

Случай (а): Параллельные прямые

1. Прямые AB и CD заданы таким образом, что углы между ними и секущей (обозначим ее EF) равны ∠ABC = 70° и ∠BCD = 110°.
2. Сумма этих углов равна 180°: 70° + 110° = 180°. Это говорит о том, что данные углы являются односторонними.
3. По признаку параллельности прямых, если сумма односторонних углов равна 180°, то прямые AB и CD параллельны.
4. Визуально это можно представить так: две прямые AB и CD никогда не пересекутся, они идут на одинаковом расстоянии друг от друга.

Случай (б): Пересекающиеся прямые

1. Прямые AB и CD пересекаются в точке E. Это возможно, если углы ∠ABC и ∠BCD являются смежными.
2. Смежные углы – это такие углы, у которых одна сторона общая, а две другие стороны являются продолжениями друг друга.
3. Сумма смежных углов равна 180°. В данном случае ∠ABC = 70°, ∠BCD = 110°, и их сумма также равна 180°.
4. Следовательно, прямые AB и CD пересекаются, образуя точку E.

Таким образом, в случае (а) прямые AB и CD параллельны, а в случае (б) они пересекаются.