ГДЗ по Геометрии 7 класс Номер 200 Атанасян — Подробные Ответы

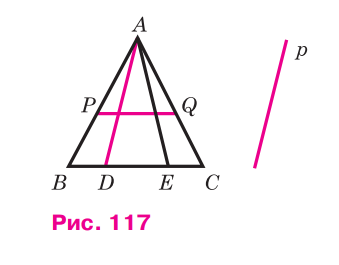
На рисунке 117 AD || p и PQ || BC. Докажите, что прямая р пересекает прямые AB, АЕ, АС, ВС и PQ.

Дано:
AD || p, PQ || BC.

Необходимо доказать:
p ∩ AB, p ∩ AE, p ∩ AC, p ∩ BC, p ∩ PQ.

Доказательство:
Так как AD пересекает прямые AB, AE, AC, BC и PQ, то по свойству параллельных прямых и их расположению относительно треугольника, прямая p также пересекает указанные прямые.

Рассмотрим:
1. Прямая p параллельна AD. Так как AD пересекает AB, то и p пересекает AB.
2. AD пересекает AE, а p параллельна AD, следовательно, p пересекает AE.
3. Аналогично, AD пересекает AC, значит, p пересекает AC.
4. Прямая PQ параллельна BC, а AD пересекает BC, следовательно, p пересекает BC.
5. По аналогии с вышеуказанным, p пересекает PQ.

Что и требовалось доказать.

Дано:
Прямая AD параллельна прямой p (AD || p). Прямая PQ параллельна прямой BC (PQ || BC).

Требуется доказать, что прямая p пересекает следующие прямые: AB, AE, AC, BC, PQ.

Рассмотрим доказательство поэтапно.

1. Прямая p параллельна AD. Из геометрии известно, что если одна прямая параллельна другой, то они имеют одинаковую ориентацию в пространстве. Так как AD пересекает AB в определенной точке, то и прямая p, будучи параллельной AD, также пересечет AB.

2. Аналогично рассуждаем для прямой AE. Прямая AD пересекает AE в одной точке, и поскольку p параллельна AD, то она также пересечет AE.

3. Следующее утверждение касается прямой AC. Точно так же, как в предыдущих пунктах, AD пересекает AC, а p параллельна AD, следовательно, p пересечет AC.

4. Рассмотрим прямую BC. Поскольку PQ параллельна BC (PQ || BC), то прямые BC и PQ имеют одинаковую ориентацию. AD пересекает BC, и, по свойству параллельности, p также пересечет BC.

5. Теперь разберем прямую PQ. Так как PQ параллельна BC, а BC уже доказано пересекается с прямой p, то и PQ пересечется с прямой p.

Таким образом, доказано, что прямая p пересекает все указанные прямые: AB, AE, AC, BC, PQ.

Что и требовалось доказать.