ГДЗ по Геометрии 7 класс Номер 20 Атанасян — Подробные Ответы

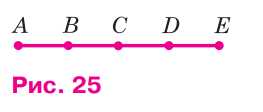
На рисунке 25 отрезки AB, BC, CD и DE равны.

Укажите:
а) середины отрезков AC, AE и CE;
б) отрезок, серединой которого является точка D;
в) отрезки, серединой которых является точка C.

а) Середины отрезков:
Середина \(AC\) — точка между \(A\) и \(C\).
Середина \(AE\) — точка между \(A\) и \(E\).
Середина \(CE\) — точка между \(C\) и \(E\).

б) Отрезок, серединой которого является точка \(D\):
Отрезок \(CE\), так как \(D\) — середина \(CD\), а \(CD = DE\).

в) Отрезки, серединой которых является точка \(C\):
Отрезок \(BC\), так как \(C\) — середина \(BC\), а \(AB = BC\).

1. Середины отрезков:
Середина отрезка \(AC\) — это точка, которая находится ровно посередине между точками \(A\) и \(C\). На рисунке она выделена красной точкой. Поскольку \(AB = BC\), то точка \(B\) является серединой \(AC\).
Середина отрезка \(AE\) — точка, находящаяся посередине между \(A\) и \(E\). Поскольку \(AB = BC = CD = DE\), отрезок \(AE\) равен сумме четырёх равных частей, и середина будет между точками \(B\) и \(D\), отмечена красной точкой.
Середина отрезка \(CE\) — точка, находящаяся посередине между \(C\) и \(E\). Отрезок \(CE\) состоит из двух равных частей \(CD\) и \(DE\), поэтому середина находится в точке \(D\), выделенной красной точкой.

2. Отрезок, серединой которого является точка \(D\):
Точка \(D\) является серединой отрезка \(CE\), так как \(CD = DE\). Следовательно, отрезок \(CE\) равен \(2 \cdot CD\), а \(D\) делит его на две равные части.

3. Отрезки, серединой которых является точка \(C\):
Точка \(C\) является серединой отрезка \(AB\), если \(AB = BC\). По условию \(AB = BC\), следовательно, \(C\) — середина отрезка \(AB\). Также \(C\) является серединой отрезка \(BC\), так как \(AB = BC\). Таким образом, отрезок \(BC\) имеет середину в точке \(C\).