
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 199 Атанасян — Подробные Ответы
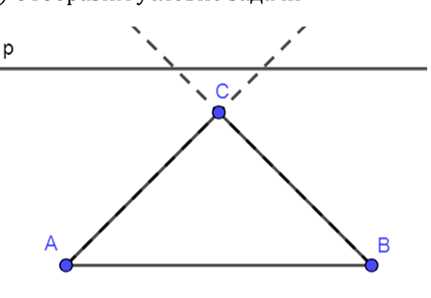
Прямая р параллельна стороне AB треугольника ABC. Докажите, что прямые ВС и АС пересекают прямую р.
Для решения задачи необходимо рассмотреть все возможные случаи относительно расположения прямой р и треугольника ABC. Мы покажем, что прямые BC и AC всегда пересекают прямую р, если она параллельна стороне AB.
Прямая р параллельна стороне AB, поэтому она не пересекает AB. Однако треугольник имеет вершины C, которые всегда находятся вне прямой AB. Таким образом, прямые BC и AC, выходящие из вершины C, обязательно пересекут прямую р.
Если прямая р находится выше треугольника (вне его), то вершина C делит плоскость на две области, и прямые BC и AC, проходя через вершины B и A, обязательно пересекают р.
Если прямая р находится ниже треугольника (вне его), аналогично, прямые BC и AC также будут пересекать р, так как вершина C соединяет две стороны треугольника.
показаны три случая расположения прямой р относительно треугольника ABC:
- Прямая р выше треугольника.
- Прямая р внутри треугольника.
- Прямая р ниже треугольника.
Во всех случаях прямые BC и AC пересекают прямую р, так как вершина C соединяет стороны треугольника, а р параллельна стороне AB.
Рассмотрим задачу, где прямая р параллельна стороне AB треугольника ABC, и требуется доказать, что прямые BC и AC пересекают прямую р. Для этого разберем задачу в общем виде с учетом всех возможных случаев расположения прямой р относительно треугольника.
1. Прямая р параллельна стороне AB. Это означает, что прямая р и сторона AB лежат на двух различных прямых, которые никогда не пересекутся. Параллельность гарантирует, что р будет проходить на фиксированном расстоянии от AB.
2. Треугольник ABC задается тремя вершинами: A, B и C. Стороны треугольника AB, BC и AC соединяют эти вершины. Прямые BC и AC выходят из вершины C и соединяются с вершинами B и A соответственно.
3. Вершина C находится вне прямой AB (так как треугольник не вырожденный). Следовательно, вершина C делит плоскость на две области, и прямые BC и AC, соединяющие C с вершинами B и A, обязательно пересекают любую прямую, параллельную AB, которая проходит через эту область.
4. Рассмотрим три возможных случая расположения прямой р относительно треугольника ABC:
— Прямая р проходит выше треугольника. В этом случае прямая р пересекает продолжения сторон BC и AC, так как вершина C находится ниже прямой р, а стороны BC и AC наклонены в направлении вершин B и A.
— Прямая р проходит внутри треугольника. В этом случае прямая р пересекает сами стороны BC и AC, так как она проходит через треугольник и делит его на части.
— Прямая р проходит ниже треугольника. В этом случае прямая р также пересекает продолжения сторон BC и AC, так как вершина C находится выше прямой р, а стороны BC и AC наклонены вниз к вершинам B и A.
5. Таким образом, независимо от положения прямой р (выше, внутри или ниже треугольника), она всегда будет пересекать прямые BC и AC. Это связано с тем, что вершина C находится вне прямой AB, а стороны BC и AC соединяют вершину C с вершинами B и A, проходя через область, в которой расположена прямая р.
6. Вывод: так как прямая р параллельна стороне AB и не совпадает с ней, она обязательно пересечет прямые BC и AC, независимо от ее положения относительно треугольника ABC.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!