ГДЗ по Геометрии 7 класс Номер 186 Атанасян — Подробные Ответы

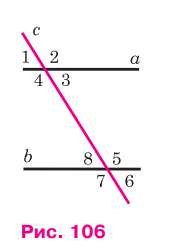
186. На рисунке 106 прямые a и b пересечены прямой c. Докажите, что a || b, если:

a) угол 1 = 37°, угол 7 = 143°;
б) угол 1 = 26°;
в) угол 1 = 45°, а угол 7 в три раза больше угла 3.

a) Углы 1 и 7 односторонние. Их сумма 37° + 143° = 180°. Следовательно, a || b.

б) Углы 1 и 6 накрест лежащие. Они равны по условию, значит, a || b.

в) Угол 7 в три раза больше угла 3. Пусть угол 3 = x, тогда угол 7 = 3x. Сумма углов 3 и 7 равна 4x = 180°, отсюда x = 45°. Угол 1 = 45°, угол 7 = 135°. Углы 1 и 7 односторонние, их сумма 180°, значит, a || b.

а) Углы 1 и 7 являются односторонними углами при пересечении прямых a и b секущей c. Для того чтобы прямые a и b были параллельны, сумма односторонних углов должна быть равна 180°. Проверим: угол 1 равен 37°, угол 7 равен 143°. Сумма этих углов составляет 37° + 143° = 180°. Таким образом, условие параллельности прямых выполняется, следовательно, a || b.

б) Углы 1 и 6 являются накрест лежащими углами при пересечении прямых a и b секущей c. Для того чтобы прямые a и b были параллельны, накрест лежащие углы должны быть равны. Условие задачи утверждает, что угол 1 равен углу 6. Так как накрест лежащие углы равны, то это доказывает, что a || b.

в) Условие задачи утверждает, что угол 1 равен 45°, а угол 7 в три раза больше угла 3. Обозначим угол 3 за x, тогда угол 7 равен 3x. Углы 3 и 7 являются односторонними углами, а их сумма должна быть равна 180° для того, чтобы прямые a и b были параллельны. Запишем уравнение: x + 3x = 180°. Решая его, получаем: 4x = 180°, отсюда x = 45°. Таким образом, угол 3 равен 45°, угол 7 равен 135°. Углы 1 и 7 также являются односторонними углами, их сумма равна 45° + 135° = 180°. Условие параллельности выполняется, следовательно, a || b.