ГДЗ по Геометрии 7 класс Номер 185 Атанасян — Подробные Ответы

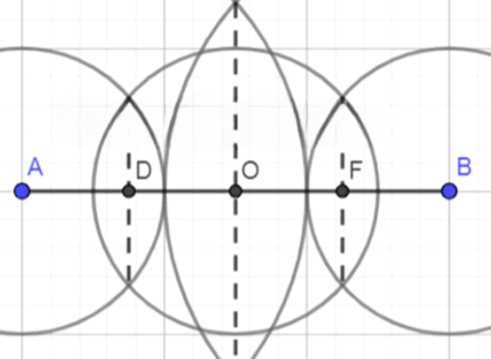
С помощью циркуля и линейки разделите данный отрезок на четыре равные части.

Для деления отрезка AB на четыре равные части:

1. Задаются точки \( A(0, 0) \) и \( B(8, 0) \).
2. Середина отрезка:
\[
\text{середина1} = \frac{A + B}{2} = (4, 0).
\]
3. Радиус первой пары окружностей:
\[
\text{радиус1} = \frac{8}{2} = 4.
\]
4. Точки деления половин:
— Левый делитель:
\[
\text{середина2} = \frac{A + \text{середина1}}{2} = (2, 0).
\]
— Правый делитель:
\[
\text{середина3} = \frac{\text{середина1} + B}{2} = (6, 0).
\]
5. Радиус второй пары окружностей:
\[
\text{радиус2} = \frac{\text{радиус1}}{2} = 2.
\]

Для деления отрезка AB на четыре равные части выполните следующие шаги:

1. Задаются точки \( A(0, 0) \) и \( B(8, 0) \). Длина отрезка AB равна 8 единиц.

2. Находим середину отрезка AB:
\[
\text{середина1} = \frac{A + B}{2} = \frac{(0, 0) + (8, 0)}{2} = (4, 0).
\]
Это точка, которая делит отрезок пополам.

3. Рассчитываем радиус первой пары окружностей, который равен половине длины отрезка AB:
\[
\text{радиус1} = \frac{8}{2} = 4.
\]
Окружности строятся с центрами в точках A и B и пересекаются в середине отрезка AB.

4. Находим точки деления половин:
— Для левой половины отрезка:
\[
\text{середина2} = \frac{A + \text{середина1}}{2} = \frac{(0, 0) + (4, 0)}{2} = (2, 0).
\]
— Для правой половины отрезка:
\[
\text{середина3} = \frac{\text{середина1} + B}{2} = \frac{(4, 0) + (8, 0)}{2} = (6, 0).
\]

5. Рассчитываем радиус второй пары окружностей, который равен половине радиуса первой пары:
\[
\text{радиус2} = \frac{\text{радиус1}}{2} = \frac{4}{2} = 2.
\]
Первая окружность строится с центром в точке A, вторая окружность — с центром в середине1.

6. Окружности с радиусом 2 пересекаются в точках деления на четверти. Эти точки соответствуют делению отрезка AB на четыре равные части.

7. Итоговые точки деления отрезка AB:
— \( A(0, 0) \)
— \( \text{середина2}(2, 0) \)
— \( \text{середина1}(4, 0) \)
— \( \text{середина3}(6, 0) \)
— \( B(8, 0) \)

На графике отображаются отрезок AB, точки деления и соответствующие окружности с пояснениями в легенде.