ГДЗ по Геометрии 7 класс Номер 182 Атанасян — Подробные Ответы

Даны прямая а, точки А, В и отрезок PQ. Постройте треугольник ABC так, чтобы вершина С лежала на прямой а и AC = PQ.

1. Постройте прямую a.
2. Найдите длину отрезка PQ.
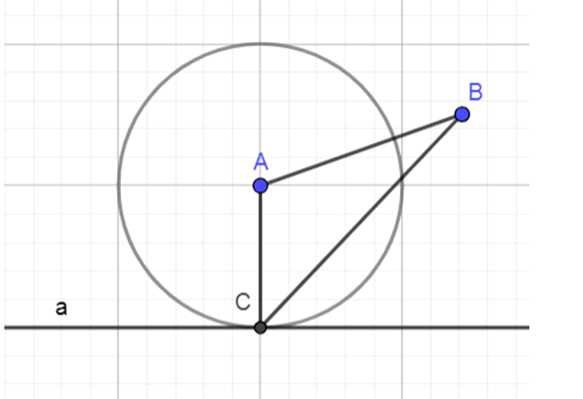
3. Постройте окружность с центром в точке A и радиусом, равным длине PQ.
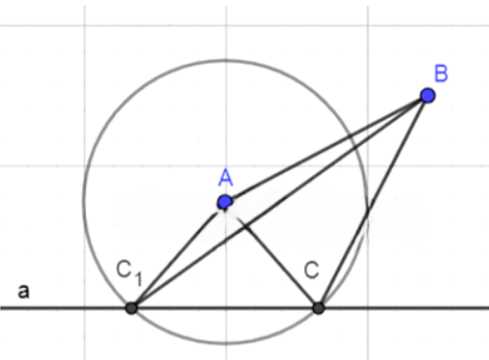
4. Найдите точки пересечения окружности с прямой a, это будут возможные положения вершины C.
5. Соедините точки A, B и каждую из найденных точек C, чтобы получить два треугольника ABC.

1. Даны прямая a, точки A и B, а также отрезок PQ. Требуется построить треугольник ABC так, чтобы вершина C лежала на прямой a, а длина AC была равна длине отрезка PQ.

2. Вычисляем длину отрезка PQ. Для этого используем формулу расстояния между двумя точками: PQ = √((x2 — x1)² + (y2 — y1)²), где (x1, y1) и (x2, y2) — координаты точек P и Q.

3. Проводим окружность с центром в точке A и радиусом, равным длине отрезка PQ. Уравнение окружности имеет вид (x — xA)² + (y — yA)² = r², где (xA, yA) — координаты точки A, а r — радиус окружности, равный длине отрезка PQ.

4. Находим точки пересечения окружности с прямой a. Уравнение прямой a задается в общем виде y = kx + b, где k — наклон прямой, а b — её свободный член. Подставляем уравнение прямой a в уравнение окружности и решаем полученное квадратное уравнение относительно x. Это дает два значения x, соответствующие точкам пересечения.

5. Для каждого найденного значения x вычисляем координаты точки пересечения, подставляя x в уравнение прямой a. Таким образом, получаем две возможные точки C1 и C2, которые лежат на прямой a и удовлетворяют условию AC = PQ.

6. Соединяем точки A, B и C1, а также точки A, B и C2. Получаем два треугольника ABC1 и ABC2, которые удовлетворяют всем условиям задачи.

7. На этом построение завершено. Треугольники ABC1 и ABC2 являются искомыми.