
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 181 Атанасян — Подробные Ответы
Постройте: а) окружность данного радиуса, проходящую через две данные точки; б) серединный перпендикуляр к отрезку с концами в этих точках.
а) Постройте окружность с центром в середине отрезка между двумя точками и радиусом, равным заданному.
б) Постройте серединный перпендикуляр, проведя прямую, перпендикулярную отрезку, проходящую через его середину.
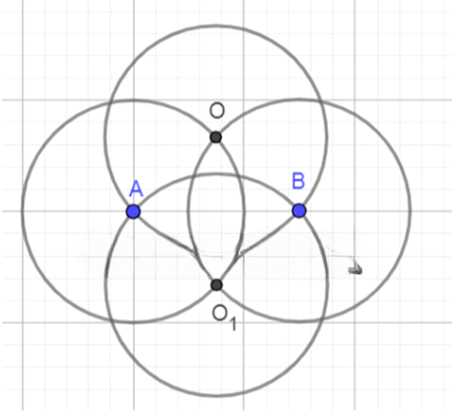
1. Даны две точки A и B.
2. Найдите середину отрезка AB. Для этого сложите координаты точек A и B по каждой оси и разделите их на два. Это будет точка M, которая является серединой отрезка.
3. Постройте серединный перпендикуляр. Для этого:
— Найдите направление отрезка AB, вычитая координаты точки A из координат точки B.
— Постройте вектор, перпендикулярный направлению AB. Для этого поменяйте местами координаты направления и измените знак одной из них. Например, если направление AB имеет координаты (x, y), то перпендикулярный вектор будет (-y, x).
— Проведите прямую через середину отрезка M в направлении этого перпендикулярного вектора.
4. Постройте окружность данного радиуса R, проходящую через точки A и B. Для этого:
— Убедитесь, что расстояние между точками A и B меньше или равно диаметру окружности (2R), иначе построить окружность невозможно.
— Найдите центр окружности. Он лежит на серединном перпендикуляре, на одинаковом расстоянии от точек A и B. Это расстояние можно вычислить с помощью теоремы Пифагора.
— Радиус окружности равен заданному значению R.
5. Постройте графически окружность с найденным центром и радиусом R.
Результат должен включать окружность, проходящую через точки A и B, и серединный перпендикуляр к отрезку AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!