ГДЗ по Геометрии 7 класс Номер 180 Атанасян — Подробные Ответы

Постройте окружность данного радиуса, проходящую через данную точку, с центром на данной прямой.

Проведите окружность с центром в точке A и радиусом R. Найдите расстояние от точки A до прямой a. Если это расстояние меньше или равно R, определите точки пересечения окружности с прямой, обозначив их как O и O1. Постройте окружности с центрами в этих точках и радиусом R. Если расстояние больше R, решение задачи невозможно.

1. Проведем окружность с центром в данной точке A и радиусом R. Эта окружность будет пересекать прямую a, если расстояние от точки A до прямой меньше или равно R. Обозначим точки пересечения окружности с прямой через O и O1.

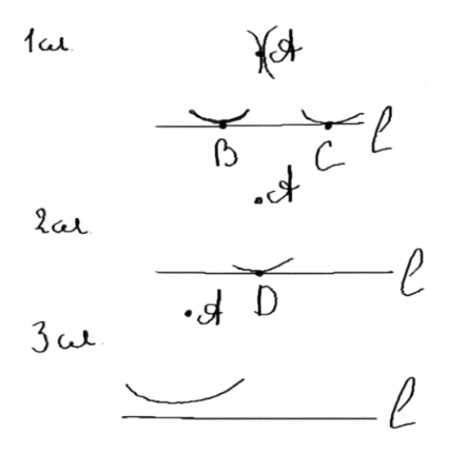
2. Рассмотрим три возможных случая:
— Если расстояние от точки A до прямой (AO) меньше R, то окружность пересечет прямую в двух точках O и O1.
— Если AO равно R, то окружность будет касаться прямой в одной точке O.
— Если AO больше R, то окружность не пересечет прямую, и задача не имеет решения.

3. В случае, если AO меньше или равно R, точки O и O1 являются возможными центрами искомой окружности.

4. Для построения окружности:
— Если AO < R, строим две окружности. Их центры находятся в точках O и O1, а радиус равен R.
— Если AO = R, строим одну окружность с центром в точке O и радиусом R.

5. Таким образом, искомая окружность будет построена в зависимости от положения точки A относительно прямой a и заданного радиуса R.