
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 178 Атанасян — Подробные Ответы
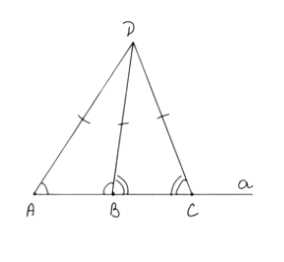
Даны три точки A, B, C, лежащие на одной прямой, и точка D, не лежащая на этой прямой. Докажите, что по крайней мере два из трёх отрезков AD, BD и CD не равны друг другу.
Допустим, что отрезки AD = BD = CD равны. Тогда треугольники ABD, ACD и BCD будут равнобедренными.
Из равенства сторон следует, что углы при основании этих треугольников также равны: ∠1 = ∠2, ∠3 = ∠4, ∠1 = ∠4. Отсюда следует, что ∠2 = ∠3. Однако углы ∠2 и ∠3 являются смежными, а сумма смежных углов равна 180°. Следовательно, ∠2 = ∠3 = 90°. Это противоречит теореме о единственности перпендикуляра, проведенного через точку, не лежащую на прямой.
Таким образом, предположение о равенстве всех трех отрезков неверно. Следовательно, по крайней мере два из трех отрезков AD, BD и CD не равны друг другу.
Рассмотрим задачу. Даны три точки A, B и C, лежащие на одной прямой, и точка D, не лежащая на этой прямой. Требуется доказать, что по крайней мере два из трех отрезков AD, BD и CD не равны друг другу.
1. Предположим, что все три отрезка равны: AD = BD = CD. Тогда треугольники ABD, ACD и BCD будут равнобедренными. Это означает, что углы при основании каждого из треугольников равны.
2. Рассмотрим треугольник ABD. Так как он равнобедренный (по предположению AD = BD), то углы при основании равны: ∠1 = ∠2.
3. Рассмотрим треугольник ACD. Он также равнобедренный (по предположению AD = CD), поэтому углы при основании равны: ∠3 = ∠4.
4. Рассмотрим треугольник BCD. Он равнобедренный (по предположению BD = CD), поэтому углы при основании равны: ∠2 = ∠3.
5. Из равенства углов ∠1 = ∠2, ∠3 = ∠4 и ∠2 = ∠3 следует, что ∠1 = ∠4.
6. Углы ∠2 и ∠3 смежные, так как они образованы прямой AC и лучом, исходящим из точки D. Сумма смежных углов равна 180°. Следовательно, если ∠2 = ∠3, то каждый из них должен быть равен 90° (∠2 = ∠3 = 90°).
7. Однако это противоречит теореме о единственном перпендикуляре. Согласно этой теореме, через точку, не лежащую на данной прямой, можно провести только один перпендикуляр к этой прямой. Если бы ∠2 = ∠3 = 90°, то через точку D проходило бы два перпендикуляра к прямой AC, что невозможно.
8. Таким образом, наше предположение о равенстве всех трех отрезков AD = BD = CD приводит к противоречию.
9. Следовательно, по крайней мере два из трех отрезков AD, BD и CD не равны друг другу. Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!