
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 173 Атанасян — Подробные Ответы
Докажите, что угол, смежный с углом треугольника, больше каждого из двух других углов треугольника.
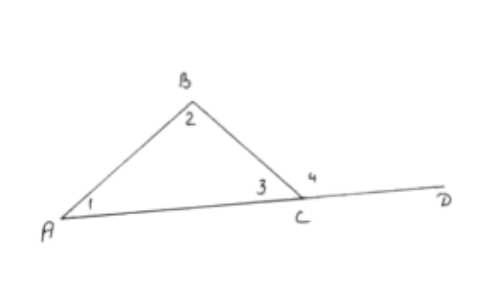
Рассмотрим треугольник и его смежный угол. Пусть один из углов треугольника равен x. Тогда смежный угол к этому углу равен 180° — x, так как сумма смежных углов равна 180°.
Теперь вспомним, что сумма всех углов треугольника равна 180°. Если один из углов треугольника равен x, то сумма двух оставшихся углов треугольника равна 180° — x.
Обозначим два других угла треугольника как α и β. Тогда выполняется равенство α + β = 180° — x.
Сравним смежный угол (180° — x) с каждым из углов треугольника. Заметим, что:
1. Смежный угол равен 180° — x.
2. Каждый из углов треугольника (в данном случае α и β) меньше суммы углов α + β, то есть меньше 180° — x.
Таким образом, смежный угол, равный 180° — x, больше каждого из углов треугольника, так как он превышает сумму двух других углов треугольника, а каждый из этих углов, в свою очередь, меньше этой суммы. Это доказывает, что смежный угол больше любого угла треугольника.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!