ГДЗ по Геометрии 7 класс Номер 169 Атанасян — Подробные Ответы

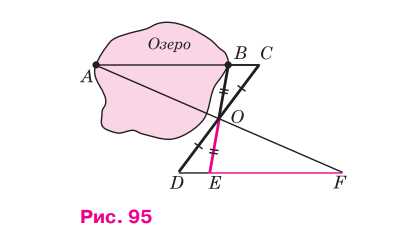
На рисунке изображены две точки O и D, которые лежат на одной линии. От точки O проведены два отрезка OB и OC, а от точки D проведены два отрезка DE и DF. Дано, что OC = OD и OB = OE. Требуется доказать, что отрезок AB равен отрезку EF, где AB и EF — это горизонтальные отрезки, соединяющие соответствующие точки на концах лучей.

Рассмотрим треугольники BOC и DOE. По условию OC = OD и OB = OE. Углы BOC и DOE равны как вертикальные. Следовательно, треугольники BOC и DOE равны по первому признаку равенства треугольников (две стороны и угол между ними). Из равенства треугольников следует, что BC = DE.

Рассмотрим треугольники AOC и DOF. По условию OC = OD, углы AOC и DOF равны как вертикальные. Также ранее доказано, что угол DOE равен углу OCB. Следовательно, треугольники AOC и DOF равны по второму признаку равенства треугольников (сторона и два прилежащих угла). Из равенства треугольников следует, что AC = DF.

Теперь выразим отрезки AB и EF. Так как AC = AB + BC и DF = DE + EF, а ранее доказано, что AC = DF и BC = DE, то AB = EF.

Способ измерения ширины озера основан на том, что отрезок EF равен отрезку AB. Для измерения ширины озера достаточно измерить EF на суше, который равен ширине озера AB.

Рассмотрим задачу подробно.

1. По условию OC = OD и OB = OE. Также даны вертикальные углы BOC и DOE.

2. Рассмотрим треугольники BOC и DOE. Эти треугольники имеют:
— OC = OD (по условию),
— OB = OE (по условию),
— угол BOC = угол DOE (как вертикальные углы).

Таким образом, треугольники BOC и DOE равны по первому признаку равенства треугольников (две стороны и угол между ними). Из равенства треугольников следует, что соответствующие стороны BC и DE равны, то есть BC = DE.

3. Теперь рассмотрим треугольники AOC и DOF. Эти треугольники имеют:
— OC = OD (по условию),
— угол AOC = угол DOF (как вертикальные углы),
— угол OCB = угол DOE (доказано ранее, так как треугольники BOC и DOE равны).

Следовательно, треугольники AOC и DOF равны по второму признаку равенства треугольников (сторона и два прилежащих угла). Из равенства треугольников следует, что соответствующие стороны AC и DF равны, то есть AC = DF.

4. Теперь выразим отрезки AB и EF через части сторон AC и DF:
— AC = AB + BC,
— DF = DE + EF.

Так как доказано, что AC = DF и BC = DE, то можно записать:
AB + BC = DE + EF.

Подставляя BC = DE, получаем:
AB = EF.

Таким образом, доказано, что AB = EF.

Способ измерения ширины озера основан на том, что отрезок EF равен отрезку AB. Чтобы измерить ширину озера (отрезок AB), достаточно перенести измерения на сушу и измерить отрезок EF, который равен AB.