
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 155 Атанасян — Подробные Ответы
Дан треугольник ABC. Постройте: а) биссектрису АK; б) медиану ВМ; в) высоту СН треугольника.
Для построения углов 45° и 22°30′ с использованием циркуля и линейки:
а) Построение угла 45°:
1. Постройте прямой угол (90°), используя перпендикулярные линии.
2. Разделите этот угол пополам, проведя биссектрису. Полученный угол будет равен 45°.
б) Построение угла 22°30′:
1. Постройте угол 45°, как описано в пункте а.
2. Разделите угол 45° пополам, проведя биссектрису. Полученный угол будет равен 22°30′.
Если нужно, могу изобразить построение. Уточните.
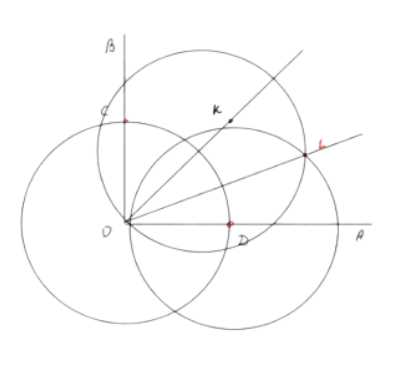
Для построения углов 45° и 22°30′ с использованием циркуля и линейки необходимо выполнить следующие действия:
а) Построение угла 45°:
1. Начертите луч, который будет одной из сторон угла. Обозначьте его, например, как OA.
2. Используя циркуль, постройте перпендикуляр к лучу OA. Для этого:
— Установите циркуль в точку O и проведите дугу произвольного радиуса, которая пересечет луч OA в точке B.
— Не изменяя радиус циркуля, установите его в точку B и проведите дугу. Затем установите циркуль в точку пересечения дуги с продолжением OA и проведите еще одну дугу. Эти две дуги пересекутся в точке C.
— Соедините точки O и C. Прямая OC будет перпендикулярна OA, а угол AOC будет равен 90°.
3. Чтобы построить угол 45°, разделите угол 90° пополам:
— Установите циркуль в точку B, проведите дугу внутри угла AOC.
— Затем установите циркуль в точку C и проведите еще одну дугу, чтобы она пересеклась с первой.
— Соедините точку пересечения дуг с точкой O. Полученный луч разделит угол AOC пополам, и угол, равный 45°, будет построен.
б) Построение угла 22°30′:
1. Постройте угол 45°, как описано выше.
2. Разделите угол 45° пополам, чтобы получить угол 22°30′:
— Установите циркуль в вершину угла O и проведите дугу, которая пересечет обе стороны угла 45° в точках D и E.
— Установите циркуль в точку D и проведите дугу внутри угла. Затем установите циркуль в точку E и проведите еще одну дугу, чтобы она пересеклась с первой.
— Соедините точку пересечения дуг с точкой O. Полученный луч разделит угол 45° пополам, и угол, равный 22°30′, будет построен.
В результате выполнения всех шагов вы получите два требуемых угла: 45° и 22°30′.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!