
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 154 Атанасян — Подробные Ответы
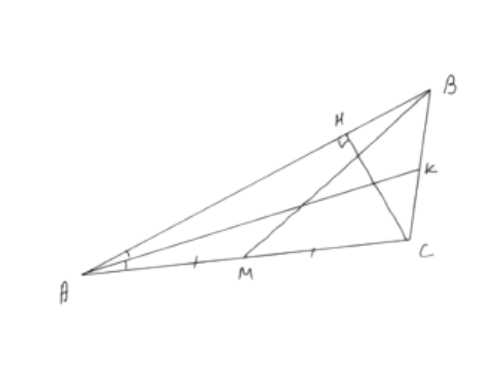
Дан треугольник ABC. Постройте: а) биссектрису АK; б) медиану ВМ; в) высоту СН треугольника.
а) Чтобы построить биссектрису AK, нужно:
1. Разделить угол A пополам.
2. Провести прямую из вершины A через точку деления угла до противоположной стороны BC. Точка пересечения будет K.
б) Чтобы построить медиану BM, нужно:
1. Найти середину стороны AC.
2. Провести прямую из вершины B к середине стороны AC. Точка пересечения будет M.
в) Чтобы построить высоту CH, нужно:
1. Провести из вершины C перпендикуляр к стороне AB.
2. Точка пересечения перпендикуляра с AB будет H.
Дан треугольник ABC. Требуется построить:
а) биссектрису AK
б) медиану BM
в) высоту CH.
Решение:
а) Построение биссектрисы AK:
1. Биссектриса треугольника — это отрезок, который делит угол пополам и соединяет вершину угла с противоположной стороной.
2. Для построения биссектрисы угла A необходимо:
— Взять транспортир и измерить угол A.
— Разделить угол A пополам, отметив точку внутри угла, через которую пройдет биссектриса.
— Провести прямую линию из вершины A через отмеченную точку до пересечения с противоположной стороной BC. Точка пересечения обозначается K.
Таким образом, AK — это биссектриса угла A.
б) Построение медианы BM:
1. Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
2. Для построения медианы BM необходимо:
— Найти середину стороны AC. Для этого измеряем длину стороны AC линейкой и делим её пополам. Обозначим середину точки AC буквой M.
— Провести прямую линию из вершины B через точку M.
Таким образом, BM — это медиана треугольника.
в) Построение высоты CH:
1. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
2. Для построения высоты CH необходимо:
— Провести из вершины C перпендикуляр к стороне AB. Для этого используем угольник или транспортир, чтобы угол между высотой и стороной AB был равен 90 градусам.
— Точка пересечения перпендикуляра с AB обозначается буквой H.
Таким образом, CH — это высота треугольника.
Итог:
В результате построений мы получили:
1. Биссектрису AK, которая делит угол A пополам.
2. Медиану BM, которая соединяет вершину B с серединой стороны AC.
3. Высоту CH, которая является перпендикуляром из вершины C на сторону AB.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!