Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
Основные особенности учебника:
- Структурированность материала:
- Учебник разделен на логические главы, каждая из которых охватывает определенную тему геометрии, что позволяет легко ориентироваться в материале.
- Доступность изложения:
- Язык и стиль написания адаптированы для школьников, что делает сложные концепции более понятными и доступными.
- Многообразие задач:
- В учебнике представлено множество задач различной сложности, что позволяет каждому ученику найти подходящие для себя упражнения и развивать свои навыки.
- Иллюстрации и схемы:
- Наглядные иллюстрации и схемы помогают лучше усвоить материал и визуализировать геометрические фигуры и их свойства.
- Практические примеры:
- Учебник включает практические примеры из реальной жизни, что делает изучение геометрии более увлекательным и актуальным.
- Поддержка для учителей:
- Включены методические рекомендации, которые помогут преподавателям эффективно использовать материал на уроках.
Заключение
Учебник Атанасяна по геометрии — это отличный инструмент для изучения предмета, который сочетает в себе доступность, разнообразие и практическую направленность. Он подходит как для самостоятельного изучения, так и для использования в классе, что делает его незаменимым помощником в образовательном процессе.
ГДЗ по Геометрии 7 класс Номер 153 Атанасян — Подробные Ответы
Даны прямая a и точка M, не лежащая на ней. Постройте прямую, проходящую через точку M и перпендикулярную к прямой a.
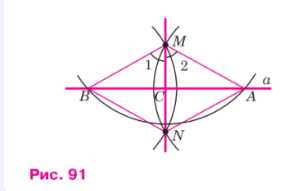
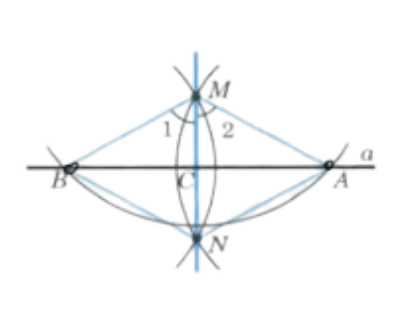
Решение: Построим окружность с центром в данной точке M, пересекающую данную прямую a в двух точках, которые обозначим буквами A и B. Затем построим две окружности с центрами A и B, проходящие через точку M. Эти окружности пересекаются в точке M и ещё в одной точке, которую обозначим буквой N. Проведём прямую MN и докажем, что эта прямая искомая, то есть она перпендикулярна к прямой a.
В самом деле, треугольники AMN и BMN равны по трём сторонам, поэтому углы 1 и 2 равны. Отсюда следует, что отрезок MC (где C — точка пересечения прямых a и MN) является биссектрисой равнобедренного треугольника AMB, а значит, и высотой. Таким образом, MN перпендикулярна AB, то есть MN перпендикулярна a.
Даны прямая a и точка M, не лежащая на ней. Построим прямую, проходящую через точку M и перпендикулярную к прямой a.
1. Построим окружность с центром в точке M, пересекающую прямую a в точках A и B.
2. Построим две окружности с центрами в точках A и B, радиус которых равен расстоянию от A до M и от B до M соответственно. Эти окружности пересекутся в точке M и еще в одной точке N.
3. Проведем прямую через точки M и N. Эта прямая будет искомой, так как она перпендикулярна прямой a.
Доказательство: Треугольники AMN и BMN равны по трем сторонам, поэтому углы при основании равны. Отсюда следует, что прямая MN является высотой треугольника AMB, а значит, перпендикулярна прямой a.
Даны прямая a и точка M, не лежащая на ней. Требуется построить прямую, проходящую через точку M и перпендикулярную к прямой a.
Решение:
1. Построим окружность с центром в точке M и произвольным радиусом, так чтобы она пересекала прямую a в двух точках. Обозначим точки пересечения этой окружности с прямой a буквами A и B.
2. Построим две окружности:
— Первая окружность с центром в точке A и радиусом, равным расстоянию от точки A до точки M.
— Вторая окружность с центром в точке B и радиусом, равным расстоянию от точки B до точки M.
3. Эти две окружности пересекутся в двух точках:
— В точке M (общая точка для обеих окружностей).
— В еще одной точке, которую обозначим буквой N.
4. Проведем прямую через точки M и N. Эта прямая будет искомой.
Доказательство:
1. Рассмотрим треугольники AMN и BMN. Они равны по трем сторонам:
— Стороны AM и BM равны, так как это радиусы окружностей, построенных с центрами в точках A и B.
— Стороны AN и BN равны, так как это радиусы окружностей, построенных с одинаковым радиусом.
— Общая сторона MN.
2. Из равенства треугольников AMN и BMN следует, что углы ∠AMN и ∠BMN равны.
3. Прямая MN делит угол AMB пополам, то есть является биссектрисой угла AMB. Поскольку треугольник AMB равнобедренный (AM = BM), биссектриса MN одновременно является высотой.
4. Высота треугольника AMB, проведенная из вершины M, перпендикулярна основанию AB, которое лежит на прямой a.
Таким образом, прямая MN перпендикулярна прямой a.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.