
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 152 Атанасян — Подробные Ответы
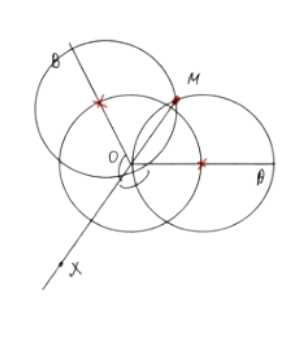
Дан тупой угол AOB. Постройте луч ОХ так, чтобы углы ХОА и ХОВ были равными тупыми углами.
Для построения луча ОХ, чтобы углы ХОА и ХОВ были равными тупыми углами, выполните следующие шаги:
1. Постройте окружность с центром в точке O произвольного радиуса.
2. Отметьте точки пересечения окружности со сторонами угла AOB, обозначив их как A и B.
3. Постройте биссектрису угла AOB. Для этого:
— Постройте две окружности одинакового радиуса с центрами в точках A и B. Радиус должен быть меньше расстояния AB.
— Обозначьте точки пересечения этих окружностей как M и N.
— Проведите прямую через точки M и N. Эта прямая является биссектрисой угла AOB.
4. Продлите биссектрису от точки O за пределы угла AOB. Это и будет искомый луч ОХ.
Теперь углы ХОА и ХОВ равны и являются тупыми.
Для построения луча ОХ, чтобы углы ХОА и ХОВ были равными тупыми углами, выполните следующие шаги:
1. Постройте угол AOB, где O — вершина угла, а OA и OB — его стороны. Убедитесь, что угол AOB тупой (больше 90°, но меньше 180°).
2. Постройте окружность произвольного радиуса с центром в точке O. Эта окружность пересечет стороны угла AOB в точках A и B.
3. Для нахождения биссектрисы угла AOB выполните следующие действия:
— Постройте окружность с центром в точке A и радиусом, равным произвольному расстоянию, которое меньше длины отрезка AB. Эта окружность пересечет окружность, построенную в шаге 2, в двух точках.
— Постройте вторую окружность с центром в точке B и таким же радиусом, как у окружности, построенной из точки A. Эта окружность также пересечет окружность, построенную в шаге 2, в двух точках.
— Отметьте точки пересечения этих двух окружностей. Обозначьте их, например, как M и N.
4. Проведите прямую через точки O, M и N. Эта прямая является биссектрисой угла AOB, так как она делит угол AOB на два равных угла.
5. Продлите биссектрису от точки O за пределы угла AOB. Полученный луч обозначьте как ОХ.
6. Теперь углы ХОА и ХОВ равны и являются тупыми. Это происходит потому, что биссектриса делит угол AOB на два равных угла, и каждый из них больше 90°, но меньше 180°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!