
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 150 Атанасян — Подробные Ответы
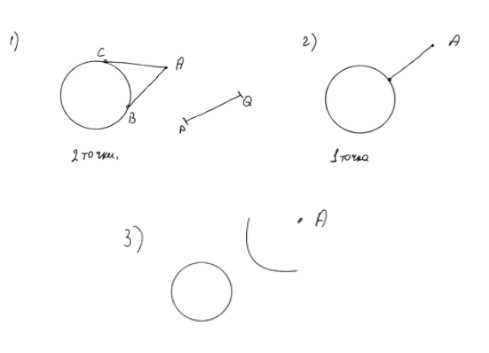
Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окружности так, чтобы AM = PQ. Всегда ли задача имеет решение?
Для решения задачи нужно построить окружность с центром в точке A и радиусом, равным длине отрезка PQ. Пересечение этой окружности с данной окружностью даст искомую точку или точки M.
Если окружности пересекаются в двух точках, то задача имеет два решения. Если окружности касаются, то решение одно. Если окружности не пересекаются, то решений нет.
Задача имеет решение, если расстояние от точки A до центра данной окружности находится между разностью и суммой радиусов двух окружностей.
Рассмотрим задачу подробно. Даны окружность, точка A, не лежащая на ней, и отрезок PQ. Требуется построить точку M на окружности так, чтобы расстояние AM было равно длине отрезка PQ. Нужно также выяснить, всегда ли задача имеет решение.
1. Построим окружность с центром в точке A и радиусом, равным длине отрезка PQ. Эта окружность будет пересекаться с данной окружностью при определенных условиях. Пересечение этих двух окружностей и даст точки, которые удовлетворяют условию задачи.
2. Рассмотрим, как взаимное расположение этих двух окружностей влияет на решение задачи.
Случай 1. Окружности пересекаются в двух точках.
Если расстояние от точки A до центра данной окружности меньше суммы радиусов двух окружностей и больше их разности, то окружности пересекутся в двух точках. В этом случае задача имеет два решения, так как существует две точки M на окружности, расстояние от которых до точки A равно длине отрезка PQ.
Случай 2. Окружности касаются друг друга.
Если расстояние от точки A до центра данной окружности равно сумме или разности радиусов двух окружностей, то окружности будут касаться друг друга. В этом случае задача имеет одно решение, так как существует единственная точка M на окружности, расстояние от которой до точки A равно длине отрезка PQ.
Случай 3. Окружности не пересекаются.
Если расстояние от точки A до центра данной окружности больше суммы радиусов двух окружностей или меньше их разности, то окружности не пересекутся. В этом случае задача не имеет решений, так как не существует точки M на окружности, удовлетворяющей условию AM = PQ.
3. Вывод.
Задача имеет решение, если расстояние от точки A до центра данной окружности находится в пределах между разностью и суммой радиусов двух окружностей. Если это расстояние выходит за указанные пределы, то задача не имеет решений.
4. Пример построения.
1) Построим окружность с центром A и радиусом, равным длине отрезка PQ.
2) Найдем точки пересечения этой окружности с данной окружностью. Эти точки пересечения будут искомыми точками M.
3) Если окружности пересекаются в двух точках, то у задачи два решения. Если они касаются, то одно решение. Если не пересекаются, то решений нет.
Таким образом, решение задачи зависит от взаимного расположения точки A, радиуса PQ и данной окружности.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!