
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 149 Атанасян — Подробные Ответы
Даны прямая а, точка В, не лежащая на ней, и отрезок PQ.
Постройте точку М на прямой а так, чтобы ВМ = PQ. Всегда ли задача имеет решение?
Для решения задачи:
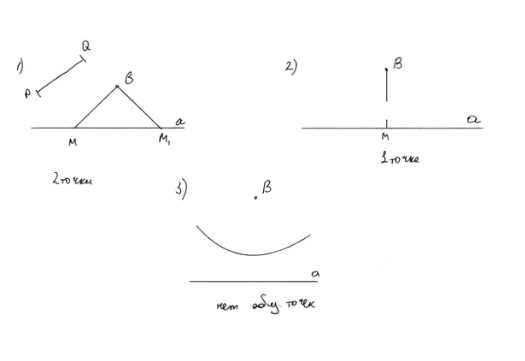
1. Рассмотрим три случая относительно расположения прямой a и точки B:
— Если точка B находится на перпендикуляре к прямой a (как в случае 2), задача имеет единственное решение. Точка M находится на пересечении перпендикуляра из B к прямой a на расстоянии, равном длине отрезка PQ.
— Если точка B не лежит на перпендикуляре к прямой a (как в случае 1), задача может иметь два решения. Построение выполняется с помощью окружностей радиуса, равного PQ, с центром в B. Эти окружности пересекают прямую a в двух точках M и M1.
— Если точка B слишком далеко от прямой a, так что радиус окружности меньше расстояния от точки B до прямой a (как в случае 3), задача не имеет решений.
2. Вывод: задача имеет решение, если расстояние от точки B до прямой a меньше или равно длине отрезка PQ. В противном случае решений нет.
Даны прямая a, точка B, не лежащая на ней, и отрезок PQ. Требуется найти точку M на прямой a так, чтобы BM = PQ, и выяснить, всегда ли задача имеет решение.
Рассмотрим задачу подробно.
1. Построим окружность с центром в точке B и радиусом, равным длине отрезка PQ. Эта окружность будет пересекаться с прямой a при определенных условиях.
2. Рассмотрим три возможных случая:
— Если расстояние от точки B до прямой a меньше длины отрезка PQ, то окружность пересечет прямую a в двух точках. В этом случае задача имеет два решения: точки M и M1.
— Если расстояние от точки B до прямой a равно длине отрезка PQ, то окружность касается прямой a в одной точке. В этом случае задача имеет одно решение: точка M.
— Если расстояние от точки B до прямой a больше длины отрезка PQ, то окружность не пересечет прямую a. В этом случае задача не имеет решений.
3. Таким образом, задача имеет решение только в том случае, если расстояние от точки B до прямой a меньше или равно длине отрезка PQ. Если это расстояние больше длины отрезка PQ, то решений нет.
Вывод: задача может иметь два решения, одно решение или не иметь решений в зависимости от взаимного расположения точки B, прямой a и длины отрезка PQ.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!