
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 145 Атанасян — Подробные Ответы
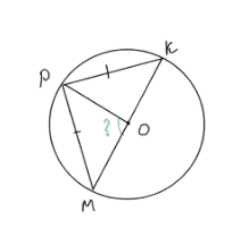
Отрезок МK — диаметр окружности с центром О, а МР и РK — равные хорды этой окружности. Найдите ∠POM.
Рассмотрим треугольник МРК. По условию МР = РК, значит треугольник МРК равнобедренный.
МО и ОК — радиусы окружности, следовательно, РО — медиана, проведенная к основанию МК. В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.
Таким образом, РО перпендикулярно МК, то есть ∠POM = 90°.
Ответ: 90°.
Дано:
Окружность с центром в точке O, отрезок MK — диаметр окружности. Хорды MP и PK равны. Найти угол ∠POM.
Решение:
1. Рассмотрим треугольник MPK. По условию MP = PK, следовательно, треугольник MPK является равнобедренным.
2. MO и OK — радиусы окружности. Так как MK — диаметр, то точка O лежит на отрезке MK, и этот отрезок делится точкой O пополам.
3. Проведем отрезок PO. Он соединяет центр окружности с точкой P.
4. В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно высотой и биссектрисой. Так как RO — медиана, проведенная к основанию MK, она будет перпендикулярна основанию.
5. Следовательно, угол ∠POM = 90°.
Ответ: 90°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!