Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 127 Атанасян — Подробные Ответы
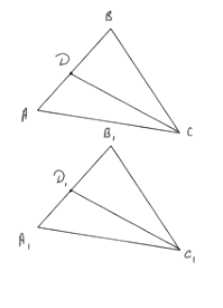
В треугольниках ABC и A1B1C1 AB = A1B1, BC = B1C1, угол B = угол B1. На сторонах AB и A1B1 отмечены точки D и D1 так, что угол ACD = угол A1C1D1. Докажите, что треугольник BCD равен треугольнику B1C1D1.
В треугольниках ABC и A1B1C1 равны соответствующие стороны AB = A1B1, BC = B1C1, а также углы ∠B = ∠B1, значит, треугольники равны. Точки D и D1 расположены так, что ∠ACD = ∠A1C1D1. Из равенства треугольников и равенства углов следует равенство четырехугольников ABCD и A1B1C1D1.
Рассмотрим задачу подробно. Даны два треугольника ABC и A1B1C1, в которых выполнены следующие условия:
- Стороны AB = A1B1 и BC = B1C1.
2. Углы ∠B = ∠B1.
3. На сторонах AB и A1B1 отмечены точки D и D1 соответственно, такие, что ∠ACD = ∠A1C1D1.
Требуется доказать, что четырехугольники ABCD и A1B1C1D1 равны. Решение:
- Из условий AB = A1B1, BC = B1C1 и ∠B = ∠B1 следует, что треугольники ABC и A1B1C1 равны по первому признаку равенства треугольников (две стороны и угол между ними равны). Это означает, что:
— AC = A1C1,
— ∠A = ∠A1,
— ∠C = ∠C1. - Рассмотрим точки D и D1, которые лежат на сторонах AB и A1B1 соответственно. По условию, углы ∠ACD и ∠A1C1D1 равны. Поскольку треугольники ABC и A1B1C1 равны, то точки D и D1 делят стороны AB и A1B1 пропорционально.
- Равенство углов ∠ACD = ∠A1C1D1 означает, что треугольники ACD и A1C1D1 подобны. Но так как AC = A1C1 и углы при вершинах равны (из равенства треугольников ABC и A1B1C1), то треугольники ACD и A1C1D1 равны.
- Аналогично, треугольники BCD и B1C1D1 равны, так как BC = B1C1, ∠BCD = ∠B1C1D1, а точки D и D1 делят стороны AB и A1B1 пропорционально.
- Из равенства треугольников ACD = A1C1D1 и BCD = B1C1D1, а также из равенства сторон AB = A1B1, BC = B1C1, AC = A1C1 следует, что четырехугольники ABCD и A1B1C1D1 равны по определению равенства многоугольников (равенство всех сторон и углов).
Таким образом, доказано, что четырехугольники ABCD и A1B1C1D1 равны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.