
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 120 Атанасян — Подробные Ответы
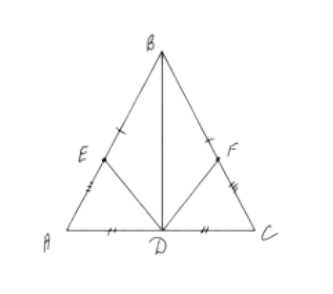
В равнобедренном треугольнике ABC с основанием AC проведена медиана BD. На сторонах AB и CB отмечены соответственно точки E и F так, что AE = CF. Докажите, что:
а) ∆BDE = ∆BDF;
б) ∆ADE = ∆CDF.
1. Дано: равнобедренный треугольник ABC с основанием AC, BD — медиана, точки E и F на сторонах AB и CB соответственно, такие что AE = CF. Требуется доказать: a) ΔBDE = ΔBDF; б) ΔADE = ΔCDF.
2. Решение:
a) ΔBDE = ΔBDF:
— В равнобедренном треугольнике медиана BD является также высотой и биссектрисой.
— Отрезки DE и DF равны, так как AE = CF и точки E и F симметричны относительно медианы BD.
— Углы BDE и BDF равны, так как медиана делит угол пополам.
— Следовательно, ΔBDE = ΔBDF по двум сторонам и углу между ними.
б) ΔADE = ΔCDF:
— AE = CF по условию.
— AD = CD, так как медиана делит основание AC пополам.
— Углы при вершинах D в треугольниках ADE и CDF равны, так как медиана является биссектрисой.
— Следовательно, ΔADE = ΔCDF по двум сторонам и углу между ними.
Доказано.
Дано: Равнобедренный треугольник ABC, где AB = BC, AC — основание. BD — медиана, проведенная к основанию AC. Точки E и F лежат на сторонах AB и CB соответственно так, что AE = CF.
Требуется доказать:
a) Треугольники BDE и BDF равны.
b) Треугольники ADE и CDF равны.
Решение:
1. Рассмотрим треугольники BDE и BDF.
— В равнобедренном треугольнике ABC медиана BD является также высотой и биссектрисой. Это означает, что медиана делит угол B пополам, а также основание AC на два равных отрезка: AD = DC.
— По условию точки E и F расположены так, что AE = CF.
— DE = DF, так как точки E и F симметричны относительно медианы BD (BD делит треугольник ABC на два равных треугольника).
— Углы BDE и BDF равны, так как медиана BD является биссектрисой угла B.
Таким образом, треугольники BDE и BDF равны по признаку равенства двух сторон и угла между ними.
2. Рассмотрим треугольники ADE и CDF.
— AE = CF по условию.
— AD = DC, так как медиана BD делит основание AC на два равных отрезка.
— Углы при вершинах D в треугольниках ADE и CDF равны, так как медиана BD является биссектрисой угла ADB и угла CDB.
Таким образом, треугольники ADE и CDF равны по признаку равенства двух сторон и угла между ними.
Вывод:
a) Треугольники BDE и BDF равны.
b) Треугольники ADE и CDF равны.
Доказательство завершено.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!