ГДЗ по Геометрии 7 класс Номер 109 Атанасян — Подробные Ответы

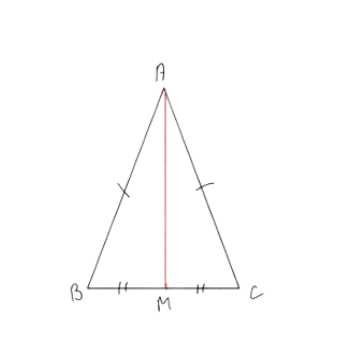
В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AM, если периметр треугольника ABC равен 32 см, а периметр треугольника ABМ равен 24 см.

Дано: равнобедренный треугольник ABC с основанием BC и медианой AM. Периметр треугольника ABC равен 32 см, периметр треугольника ABM равен 24 см.

Обозначим стороны: \(AB = AC = x\), \(BC = y\), медиана \(AM\) делит \(BC\) пополам, значит \(BM = \frac{y}{2}\).

Периметр треугольника ABC: \(AB + AC + BC = 32\). Подставим: \(x + x + y = 32\), откуда \(2x + y = 32\). Выразим \(y\): \(y = 32 — 2x\).

Периметр треугольника ABM: \(AB + BM + AM = 24\). Подставим: \(x + \frac{y}{2} + AM = 24\). Подставим \(y = 32 — 2x\):

\(x + \frac{32 — 2x}{2} + AM = 24\).

Упростим:

\(x + 16 — x + AM = 24\),

получаем

\(16 + AM = 24\),

откуда

\(AM = 8\).

Ответ: медиана AM равна 8 см.

1. Дано: равнобедренный треугольник ABC с основанием BC и медианой AM. Периметр треугольника ABC равен 32 см, периметр треугольника ABM равен 24 см. Найти медиану AM.

2. Обозначим стороны: \(AB = AC = x\), \(BC = y\). Медиана AM делит основание BC пополам, значит \(BM = MC = \frac{y}{2}\).

3. Периметр треугольника ABC равен сумме всех его сторон:

\(AB + AC + BC = 32\).

Подставим обозначения:

\(x + x + y = 32\),

откуда

\(2x + y = 32\).

Выразим \(y\):

\(y = 32 — 2x\).

4. Периметр треугольника ABM равен сумме его сторон:

\(AB + BM + AM = 24\).

Подставим обозначения:

\(x + \frac{y}{2} + AM = 24\).

5. Подставим выражение для \(y\):

\(x + \frac{32 — 2x}{2} + AM = 24\).

6. Упростим дробь:

\(x + 16 — x + AM = 24\).

7. Сложим подобные члены:

\(16 + AM = 24\).

8. Выразим медиану AM:

\(AM = 24 — 16\),

получаем

\(AM = 8\).

9. Проверка: все вычисления корректны, условия задачи выполнены.

10. Ответ: медиана AM равна 8 см.