ГДЗ по Геометрии 7 класс Номер 108 Атанасян — Подробные Ответы

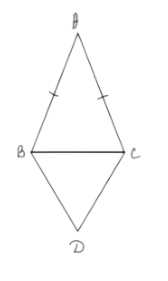
Периметр равнобедренного треугольника
ABC с основанием ВС равен 40 см, а периметр равностороннего треугольника BCD равен 45 см. Найдите стороны AB и ВС.

Периметр равнобедренного треугольника ABC равен 40 см. Пусть боковые стороны AB и AC равны \(x\), а основание BC равно \(y\). Тогда уравнение для периметра: \(2x + y = 40\).

Периметр равностороннего треугольника BCD равен 45 см, все стороны равны, значит \(BC = CD = BD = y\). Уравнение для периметра: \(3y = 45\). Отсюда \(y = \frac{45}{3} = 15\).

Подставляем \(y = 15\) в уравнение для треугольника ABC: \(2x + 15 = 40\). Решаем: \(2x = 40 — 15\), \(2x = 25\), \(x = \frac{25}{2} = 12.5\).

Ответ: боковые стороны AB и AC равны 12.5 см, основание BC равно 15 см.

Периметр равнобедренного треугольника ABC равен 40 см. В равнобедренном треугольнике две боковые стороны равны, поэтому обозначим боковые стороны AB и AC через \(x\), а основание BC через \(y\). Периметр треугольника — это сумма всех его сторон, значит уравнение для периметра можно записать как \(2x + y = 40\). Здесь \(2x\) — сумма двух равных боковых сторон, а \(y\) — основание.

Теперь рассмотрим равносторонний треугольник BCD, у которого все три стороны равны. Его периметр равен 45 см, значит каждая сторона равна одной трети периметра. Обозначим сторону равностороннего треугольника как \(y\), так как основание BC у треугольника ABC совпадает с одной из сторон треугольника BCD. Уравнение для периметра будет \(3y = 45\). Решая это уравнение, получаем \(y = \frac{45}{3} = 15\). Таким образом, основание BC равно 15 см.

Подставляем найденное значение \(y = 15\) в уравнение для периметра равнобедренного треугольника ABC: \(2x + 15 = 40\). Вычитаем 15 из обеих частей уравнения: \(2x = 40 — 15\), то есть \(2x = 25\). Чтобы найти \(x\), делим обе части уравнения на 2: \(x = \frac{25}{2} = 12.5\). Следовательно, боковые стороны AB и AC равны 12.5 см, а основание BC равно 15 см.