
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 104 Атанасян — Подробные Ответы
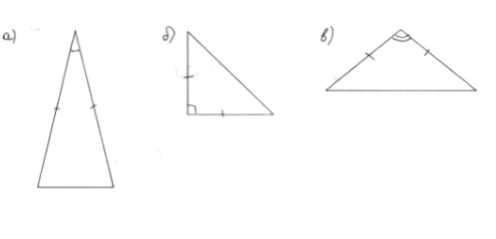
Начертите три равнобедренных треугольника так, чтобы угол, лежащий против основания, был:
а) острым; б) прямым; в) тупым.
а) Острый угол: равнобедренный треугольник, у которого угол напротив основания меньше 90 градусов. Все углы острые.
б) Прямой угол: равнобедренный треугольник, у которого угол напротив основания равен 90 градусов. Основание является гипотенузой.
в) Тупой угол: равнобедренный треугольник, у которого угол напротив основания больше 90 градусов. Боковые стороны длиннее основания.
Решение задачи заключается в построении трех равнобедренных треугольников, у которых угол напротив основания будет острым, прямым и тупым. Рассмотрим каждый случай подробно:
а) Угол напротив основания острый
Для построения равнобедренного треугольника с острым углом напротив основания необходимо, чтобы все углы треугольника были меньше 90 градусов. Это возможно, если длина боковых сторон больше длины основания. Например, пусть основание равно 6 см, а боковые стороны равны по 8 см. Построив такой треугольник, мы получим равнобедренный треугольник с острым углом напротив основания.
б) Угол напротив основания прямой
Для построения равнобедренного треугольника с прямым углом напротив основания необходимо, чтобы угол между двумя боковыми сторонами был равен 90 градусов. В этом случае основание треугольника будет гипотенузой, а боковые стороны будут равны. Например, пусть боковые стороны равны 5 см. Построив такой треугольник, мы получим равнобедренный треугольник с прямым углом напротив основания.
в) Угол напротив основания тупой
Для построения равнобедренного треугольника с тупым углом напротив основания необходимо, чтобы угол между боковыми сторонами был больше 90 градусов. Это возможно, если длина боковых сторон меньше суммы основания и одной из боковых сторон, но больше длины основания. Например, пусть основание равно 6 см, а боковые стороны равны по 7 см. Построив такой треугольник, мы получим равнобедренный треугольник с тупым углом напротив основания.
Таким образом, для каждого из случаев необходимо учитывать соотношение сторон треугольника и угол между боковыми сторонами.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!