
Учебник по геометрии для 7-9 классов авторства Атанасяна — это не просто пособие, а настоящая находка для школьников и преподавателей. Он предлагает систематизированный подход к изучению геометрии, который помогает развивать логическое мышление и пространственное восприятие.
ГДЗ по Геометрии 7 класс Номер 103 Атанасян — Подробные Ответы
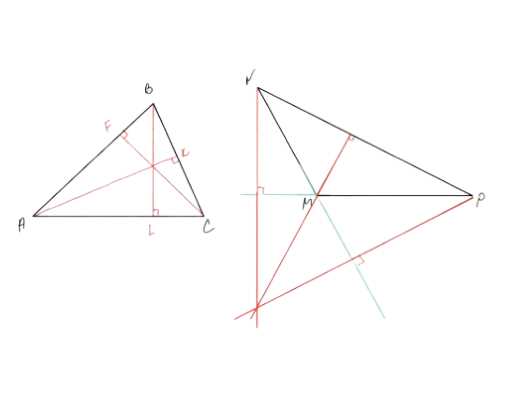
Начертите треугольник ABC с тремя острыми углами и треугольник MNP, у которого угол М тупой. С помощью чертёжного угольника проведите высоты каждого треугольника.
Для треугольника ABC с острыми углами высоты пересекаются внутри треугольника. Для треугольника MNP с тупым углом одна из высот пересекает продолжение стороны, а не сам треугольник. Высоты проведены с использованием перпендикуляров к сторонам из противоположных вершин.
Для построения треугольников с высотами выполнены следующие шаги:
1. Построен треугольник ABC с тремя острыми углами. Этот треугольник имеет все углы острыми, что позволяет высотам пересекаться внутри треугольника.
2. Для треугольника ABC проведены высоты:
— Высота из первой вершины перпендикулярна противоположной стороне и пересекает ее.
— Высота из второй вершины перпендикулярна противоположной стороне и пересекает ее.
— Высота из третьей вершины перпендикулярна противоположной стороне и пересекает ее.
3. Построен треугольник MNP с тупым углом. Этот треугольник имеет один тупой угол, что приводит к тому, что одна из высот пересекает продолжение стороны, а не сам треугольник.
4. Для треугольника MNP проведены высоты:
— Высота из первой вершины перпендикулярна противоположной стороне и пересекает ее.
— Высота из второй вершины перпендикулярна противоположной стороне и пересекает ее.
— Высота из третьей вершины перпендикулярна продолжению противоположной стороны и пересекает ее.
5. Все построения выполнены с использованием перпендикуляров из вершин треугольников к противоположным сторонам или их продолжениям.
6. На графике треугольники выделены разными цветами, и высоты показаны пунктирными линиями для наглядности.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!