ГДЗ по Геометрии 7 класс Номер 101 Атанасян — Подробные Ответы

Начертите треугольник. С помощью масштабной линейки отметьте середины сторон и проведите медианы треугольника.

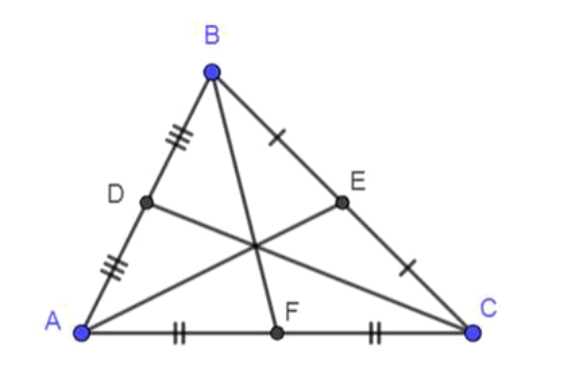
На чертеже изображен треугольник. Найдены середины его сторон, и через них проведены медианы, соединяющие вершины треугольника с противоположными серединами сторон.

1. Начертить треугольник с заданными вершинами. Пусть вершины треугольника обозначены как A, B и C. Например, координаты точек: A(0, 0), B(6, 0), C(3, 5).

2. Определить середины сторон треугольника. Для этого нужно использовать формулу нахождения середины отрезка:
M_AB = ((x1 + x2) / 2, (y1 + y2) / 2),
где x1, y1 и x2, y2 — координаты концов отрезка.
— Середина стороны AB: M_AB = ((0 + 6) / 2, (0 + 0) / 2) = (3, 0).
— Середина стороны BC: M_BC = ((6 + 3) / 2, (0 + 5) / 2) = (4.5, 2.5).
— Середина стороны CA: M_CA = ((3 + 0) / 2, (5 + 0) / 2) = (1.5, 2.5).

3. Провести медианы треугольника. Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
— Медиана из вершины A проходит через точку M_BC (середину стороны BC).
— Медиана из вершины B проходит через точку M_CA (середину стороны CA).
— Медиана из вершины C проходит через точку M_AB (середину стороны AB).

4. Построить график треугольника и медиан. На чертеже:
— Вершины треугольника обозначаются точками A, B, C.
— Середины сторон обозначаются точками M_AB, M_BC, M_CA.
— Медианы изображаются пунктирными линиями, соединяющими вершины с противоположными серединами сторон.

5. Проверить, что медианы пересекаются в одной точке — это называется центроид или центр тяжести треугольника. Он делит каждую медиану в отношении 2:1, считая от вершины.

Таким образом, треугольник построен, середины сторон найдены, медианы проведены и отмечены на графике.