
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 953 Атанасян — Подробные Ответы
Докажите, что сумма квадратов всех сторон параллелограмма равна сумме квадратов его диагоналей.
Решение
Пусть \(ABCD\) — данный параллелограмм. Введём прямоугольную систему координат так, как показано на рисунке 283.
Если \(AD = BC = a\), а точка \(B\) имеет координаты \((b; c)\), то точка \(D\) имеет координаты \((a; 0)\), а точка \(C\) — координаты \((a + b; c)\). Используя формулу расстояния между двумя точками, находим:
\(
AB^2 = b^2 + c^2, \quad AD^2 = a^2, \quad AC^2 = (a + b)^2 + c^2, \quad BD^2 = (a — b)^2 + c^2.
\)
Отсюда получаем:
\(
AB^2 + BC^2 + CD^2 + DA^2 = 2 (AB^2 + AD^2) = 2 (a^2 + b^2 + c^2),
\)
\(
AC^2 + BD^2 = (a + b)^2 + c^2 + (a — b)^2 + c^2 = 2 (a^2 + b^2 + c^2).
\)
Таким образом,
\(
AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2,
\)
что и требовалось доказать.
Для доказательства утверждения о параллелограмме используем координатный метод. Пусть параллелограмм \(ABCD\) имеет стороны \(AD = BC = a\), а точки имеют координаты: \(A(0,0)\), \(B(b,c)\), \(C(a+b,c)\), \(D(a,0)\).
Вычислим квадрат длины каждой стороны и диагонали:
1. \(AB^2 = b^2 + c^2\)
2. \(AD^2 = a^2\)
3. \(BC^2 = a^2\)
4. \(CD^2 = b^2 + c^2\)
Сумма квадратов сторон:
\(
AB^2 + BC^2 + CD^2 + DA^2 = 2(a^2 + b^2 + c^2)
\)
Теперь вычислим квадраты диагоналей:
1. \(AC^2 = (a+b)^2 + c^2 = a^2 + 2ab + b^2 + c^2\)
2. \(BD^2 = (a-b)^2 + c^2 = a^2 — 2ab + b^2 + c^2\)
Сумма квадратов диагоналей:
\(
AC^2 + BD^2 = (a^2 + 2ab + b^2 + c^2) + (a^2 — 2ab + b^2 + c^2) = \)
\(=2(a^2 + b^2 + c^2)\)
Таким образом, сумма квадратов сторон равна сумме квадратов диагоналей:
\(
AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2
\)
Пусть \(ABCD\) — параллелограмм. Введём прямоугольную систему координат. Обозначим вершины параллелограмма следующим образом: \(A(0, 0)\), \(B(b, c)\), \(C(a + b, c)\), \(D(a, 0)\), где \(a\) и \(b\) — длины сторон, а \(c\) — высота, соответствующая стороне \(a\).
Воспользуемся формулой расстояния между двумя точками для вычисления квадратов длин сторон и диагоналей.
1. Найдём квадрат длины стороны \(AB\):
\(
AB^2 = b^2 + c^2
\)
2. Найдём квадрат длины стороны \(BC\):
\(
BC^2 = a^2
\)
3. Найдём квадрат длины стороны \(CD\):
\(
CD^2 = b^2 + c^2
\)
4. Найдём квадрат длины стороны \(DA\):
\(
DA^2 = a^2
\)
Сумма квадратов всех сторон:
\(
AB^2 + BC^2 + CD^2 + DA^2 = (b^2 + c^2) + a^2 + (b^2 + c^2) + a^2 =\)
\(= 2(a^2 + b^2 + c^2)
\)
Теперь найдём квадраты диагоналей.
1. Найдём квадрат длины диагонали \(AC\):
\(
AC^2 = (a + b)^2 + c^2 = a^2 + 2ab + b^2 + c^2
\)
2. Найдём квадрат длины диагонали \(BD\):
\(
BD^2 = (a — b)^2 + c^2 = a^2 — 2ab + b^2 + c^2
\)
Сумма квадратов диагоналей:
\(
AC^2 + BD^2 = (a^2 + 2ab + b^2 + c^2) + (a^2 — 2ab + b^2 + c^2)
\)
\(
AC^2 + BD^2 = 2a^2 + 2b^2 + 2c^2 = 2(a^2 + b^2 + c^2)
\)
Таким образом, сумма квадратов всех сторон равна сумме квадратов диагоналей:
\(
AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2
\)
Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


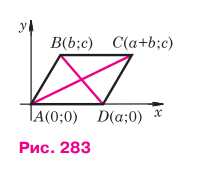

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!