Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 929 Атанасян — Подробные Ответы
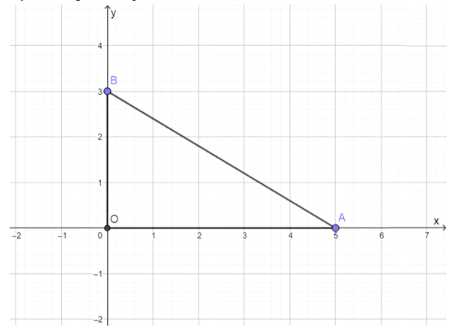
Точка А лежит на положительной полуоси Ох, а точка В — на положительной полуоси Оу. Найдите координаты вершин треугольника АВО, если: а) ОА = 5, ОВ = 3; б) ОА = а, OB = b.
Для нахождения координат вершин треугольника АВО:
1. Точка A лежит на положительной полуоси Ox, а точка B на положительной полуоси Oy.
2. Вариант а) Если \( OA = 5 \) и \( OB = 3 \):
— Координаты точки A: \( A(5, 0) \)
— Координаты точки B: \( B(0, 3) \)
3. Вариант б) Если \( OA = a \) и \( OB = b \):
— Координаты точки A: \( A(a, 0) \)
— Координаты точки B: \( B(0, b) \)
Таким образом, в каждом случае координаты определяются расстоянием от начала координат до точки на соответствующей оси.
Для решения задачи о нахождении координат вершин треугольника АВО, расположенного в системе координат, где точка A лежит на положительной полуоси Ox, а точка B на положительной полуоси Oy, рассмотрим оба варианта.
Вариант а) ОА = 5, ОВ = 3
1. Точка A находится на оси Ox, поэтому ее координаты имеют вид (x, 0). Так как расстояние ОА равно 5, это значит, что x = 5. Таким образом, координаты точки A: \( A(5, 0) \).
2. Точка B находится на оси Oy, поэтому ее координаты имеют вид (0, y). Так как расстояние ОВ равно 3, это значит, что y = 3. Таким образом, координаты точки B: \( B(0, 3) \).
3. Точка O — начало координат, поэтому она имеет координаты \( O(0, 0) \).
Таким образом, треугольник АВО имеет вершины с координатами: \( A(5, 0) \), \( B(0, 3) \), \( O(0, 0) \).
Вариант б) ОА = a, OB = b
1. Точка A находится на оси Ox, поэтому ее координаты имеют вид (x, 0). Так как расстояние ОА равно a, это значит, что x = a. Таким образом, координаты точки A: \( A(a, 0) \).
2. Точка B находится на оси Oy, поэтому ее координаты имеют вид (0, y). Так как расстояние ОВ равно b, это значит, что y = b. Таким образом, координаты точки B: \( B(0, b) \).
3. Точка O — начало координат, поэтому она имеет координаты \( O(0, 0) \).
Таким образом, треугольник АВО имеет вершины с координатами: \( A(a, 0) \), \( B(0, b) \), \( O(0, 0) \).
В обоих случаях для нахождения координат точек A и B используется свойство того, что они лежат на соответствующих осях координат, и их положение определяется расстоянием от начала координат.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.