
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 869 Атанасян — Подробные Ответы
Постройте точку, принадлежащую большему основанию равнобедренной трапеции и отстоящую от данной боковой стороны в \( n \) раз дальше, чем от другой (\( n = 2, 3, 4 \)).
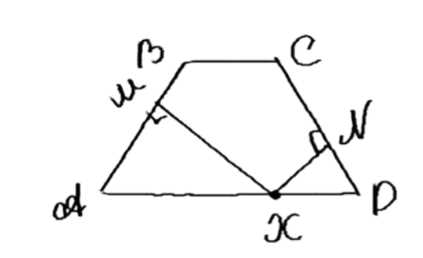
Дано: \(ABCD\) — равнобедренная трапеция, \(AD \parallel BC\), \(AD > BC\), \(AB = CD\). Необходимо построить точку \(X \in AD\), такую что \(d(X, AB) = n \cdot d(X, CD)\), где \(n = 2, 3, 4\).
Решение:
1. Рассмотрим треугольники \(\triangle AEX\) и \(\triangle DFX\). Они подобны по двум углам: \(\angle A = \angle D\) (из равнобедренности трапеции), \(\angle AEX = \angle DFX = 90^\circ\). Следовательно, коэффициент подобия \(k = \frac{XE}{XF} = n\).
2. Из подобия следует, что точка \(X\) делит отрезок \(AD\) в отношении \(AX : XD = n : 1\). Таким образом, задача сводится к разбиению отрезка \(AD\) на \(n + 1\) равных частей.
3. Для разбиения используем теорему Фалеса:
— Отложим от точки \(A\) произвольный луч \(AM\) под острым углом к \(AD\).
— На луче \(AM\) отложим \(n + 1\) равных отрезков \(AA_1 = A_1A_2 = \dots = A_{n-1}A_n\).
— Проведем прямую \(A_nD\) и параллельную ей прямую \(A_{n-1}X\). Точка пересечения \(X\) с \(AD\) будет искомой.
Точка \(X\) построена.
Дано: ABCD — равнобедренная трапеция, AD || BC, AD > BC, AB = CD. Необходимо построить точку X ∈ AD, такую что d(X, AB) = n ⋅ d(X, CD), где n = 2, 3, 4.
Решение:
1. Рассмотрим треугольники AEX и DFX. Эти треугольники подобны по двум углам:
∠A = ∠D (из равнобедренности трапеции),
∠AEX = ∠DFX = 90°.
Следовательно, ΔAEX ∼ ΔDFX.
2. Из подобия треугольников следует, что коэффициент подобия k равен отношению высот:
k = XE / XF = n.
Таким образом, точка X делит отрезок AD в отношении AX : XD = n : 1.
3. Для нахождения точки X задача сводится к разбиению отрезка AD на n + 1 равных частей. Это разбиение выполняется с использованием теоремы Фалеса.
4. Построение точки X:
а) Отложим от точки A вниз произвольный луч AM под острым углом к AD.
б) На луче AM отложим n + 1 равных отрезков AA₁ = A₁A₂ = … = Aₙ₋₁Aₙ. Для этого можно использовать линейку или циркуль.
в) Проведем прямую AₙD.
г) Проведем прямую, параллельную AₙD, из точки Aₙ₋₁. Эта прямая пересечет отрезок AD в точке X.
5. Точка X является искомой, так как ее положение удовлетворяет условию задачи: d(X, AB) = n ⋅ d(X, CD).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!