ГДЗ по Геометрии 9 класс Номер 858 Атанасян — Подробные Ответы

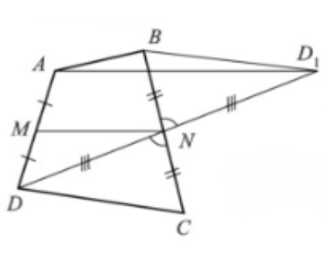
Докажите, что если противоположные стороны выпуклого четырёхугольника не параллельны, то их полусумма больше отрезка, соединяющего середины двух других противоположных сторон. 

Дано: ABCD — выпуклый четырехугольник. Условия: AD ≠ BC, AD > BC, AB ≠ CD, AB < CD, точка M принадлежит стороне AB, AM = MB, точка N принадлежит стороне CD, CN = ND. Требуется доказать, что MN < (AD + BC) / 2.

Решение:

1. Отобразим точку \( A \) относительно точки \( N \) как центра симметрии и получим точку \( A_1 \).
2. Рассмотрим треугольник \( \triangle ABA_1 \), в котором \( AM = MB \), \( AN = NA_1 \). Тогда \( MN \) является средней линией этого треугольника, а \( A_1B = 2MN \).
3. В треугольниках \( \triangle ADN \) и \( \triangle A_1CN \) видим:
\( AN = NA_1 \), \( DN = NC \), вертикальные углы равны (\( \angle AND = \angle A_1NC \)).
По первому признаку равенства треугольников \( \triangle ADN = \triangle A_1CN \), следовательно, \( A_1C = AD \).
4. В треугольнике \( \triangle CBA_1 \), по неравенству треугольника, получаем:
\( A_1B (= 2MN) < BC + A_1C (= AD) \).
Отсюда: \( 2MN < AD + BC \).
Делим обе стороны на 2:
\( MN < \frac{AD + BC}{2} \).

Доказательство завершено.

Дано: ABCD — выпуклый четырехугольник. Условия: AD ≠ BC, AD > BC, AB ≠ CD, AB < CD, точка M принадлежит стороне AB, AM = MB, точка N принадлежит стороне CD, CN = ND. Требуется доказать, что MN < (AD + BC) / 2.

Решение:

1. Рассмотрим симметрию относительно точки \( N \). Отобразим точку \( A \) относительно точки \( N \), которая является центром симметрии, и обозначим полученную точку через \( A_1 \).
Симметрия относительно точки \( N \) означает, что отрезки \( AN \) и \( NA_1 \) равны, то есть \( AN = NA_1 \).

2. Рассмотрим треугольник \( \triangle ABA_1 \), в котором выполняются следующие условия:
\( AM = MB \) (по условию задачи),
\( AN = NA_1 \) (по построению симметрии).
Тогда \( MN \) является средней линией этого треугольника. По свойству средней линии треугольника она параллельна основанию и равна половине длины основания. Таким образом,
\( MN = \frac{A_1B}{2} \).

3. Рассмотрим треугольники \( \triangle ADN \) и \( \triangle A_1CN \). В этих треугольниках:
\( AN = NA_1 \) (по построению),
\( DN = NC \) (по условию задачи),
вертикальные углы \( \angle AND \) и \( \angle A_1NC \) равны.
Следовательно, треугольники \( \triangle ADN \) и \( \triangle A_1CN \) равны по первому признаку равенства треугольников (две стороны и угол между ними).
Из равенства треугольников следует, что \( A_1C = AD \).

4. Теперь рассмотрим треугольник \( \triangle CBA_1 \). В этом треугольнике по неравенству треугольника выполняется:
\( A_1B < BC + A_1C \).
Подставим \( A_1C = AD \) из предыдущего шага:
\( A_1B < BC + AD \).

5. Поскольку \( MN = \frac{A_1B}{2} \), умножим обе части неравенства на \( \frac{1}{2} \):
\( MN = \frac{A_1B}{2} < \frac{BC + AD}{2} \).

Таким образом, доказано, что \( MN < \frac{AD + BC}{2} \).

Доказательство завершено.