
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 848 Атанасян — Подробные Ответы
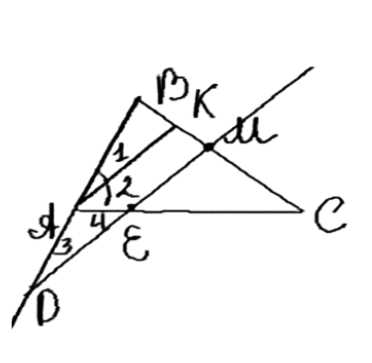
В треугольнике \( ABC \) (\( AB \neq AC \)) через середину \( M \) стороны \( BC \) проведена прямая, параллельная биссектрисе угла \( A \), которая пересекает прямые \( AB \) и \( AC \) соответственно в точках \( D \) и \( E \). Докажите, что \( BD = CE \).
Дано: ΔABC (AB ≠ AC); M ∈ BC; BM = MC; AF — биссектриса угла ∠A; MD ⊥ AF; D ∈ AB; F = MD ∩ AC.
Доказать: BD = CE.
Решение:
1. Рассмотрим треугольник DAE. Так как MD ⊥ AF, то \(\angle ADE = \angle BAF = \frac{\angle A}{2}\).
Угол \(\angle DAE = 180^\circ — \angle A\), поэтому:
\(
\angle AED = 180^\circ — (180^\circ — \angle A + \frac{\angle A}{2}) = \frac{\angle A}{2}.
\)
Следовательно, треугольник DAE равнобедренный, где DE — основание, а AD = AE.
2. Пусть BM = MC = \(d\), FM = \(f\). Тогда MD ⊥ AF, угол \(\angle B\) общий для треугольников ABF и DMB.
Из подобия треугольников ABF и DMB:
\(
k_1 = \frac{BA}{BD} = \frac{BF}{BM} = \frac{d — f}{d}.
\)
Получаем:
\(
AD = BD — BA = BD \cdot (1 — \frac{d — f}{d}) = BD \cdot \frac{f}{d}.
\)
3. Рассмотрим два других подобных треугольника: MD ⊥ AF, угол \(\angle B\) общий для треугольников MCE и FCA.
Из подобия треугольников MCE и FCA:
\(
k_2 = \frac{CE}{CA} = \frac{CM}{CF} = \frac{d}{d + f}.
\)
Отсюда:
\(
AE = CA — CE = \left(\frac{d + f}{d} — 1\right) \cdot CE = \frac{f}{d} \cdot CE.
\)
4. Вывод:
\(
AD = AE,\quad BD = CE.
\)
Следовательно, \(BD = CE\).
Дано: ΔABC (AB ≠ AC); M ∈ BC; BM = MC; AF — биссектриса угла ∠A; MD ⊥ AF; D ∈ AB; F = MD ∩ AC.
Доказать: BD = CE.
Решение:
1. Рассмотрим треугольник DAE.
Так как MD ⊥ AF, то угол \(\angle ADE = \angle BAF = \frac{\angle A}{2}\).
Угол \(\angle DAE = 180^\circ — \angle A\).
Следовательно, угол \(\angle AED\) равен:
\(
\angle AED = 180^\circ — (180^\circ — \angle A + \frac{\angle A}{2}) = \frac{\angle A}{2}.
\)
Таким образом, треугольник DAE равнобедренный, где DE — основание, а AD = AE.
2. Пусть BM = MC = \(d\), FM = \(f\).
Рассмотрим треугольники ABF и DMB.
MD ⊥ AF, угол \(\angle B\) общий для этих треугольников.
Из подобия треугольников ABF и DMB:
\(
\frac{BA}{BD} = \frac{BF}{BM}.
\)
Подставляем значения:
\(
\frac{BA}{BD} = \frac{d — f}{d}.
\)
Выразим AD через BD:
\(
AD = BD — BA = BD \cdot (1 — \frac{d — f}{d}) = BD \cdot \frac{f}{d}.
\)
3. Рассмотрим треугольники MCE и FCA.
MD ⊥ AF, угол \(\angle B\) общий для этих треугольников.
Из подобия треугольников MCE и FCA:
\(
\frac{CE}{CA} = \frac{CM}{CF}.
\)
Подставляем значения:
\(
\frac{CE}{CA} = \frac{d}{d + f}.
\)
Выразим AE через CE:
\(
AE = CA — CE = \left(\frac{d + f}{d} — 1\right) \cdot CE = \frac{f}{d} \cdot CE.
\)
4. Так как AD = AE, то:
\(
BD = CE.
\)
Следовательно, доказано, что \(BD = CE\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!