ГДЗ по Геометрии 9 класс Номер 815 Атанасян — Подробные Ответы

Докажите, что в любом четырёхугольнике какие-то две противоположные вершины лежат по разные стороны от прямой, проходящей через две другие вершины.  

Дано: ABCD — четырехугольник.
Доказать: точки \( B \) и \( D \) лежат по разные стороны от прямой \( AC \).

Решение:
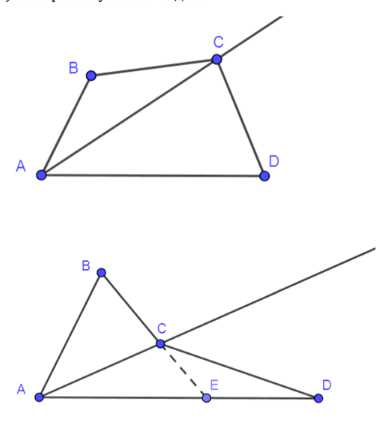
1) Предположим, что четырехугольник ABCD — выпуклый. Точки \( C \) и \( D \) лежат по одну сторону от прямой \( AB \), а точки \( C \) и \( B \) лежат по одну сторону от прямой \( AD \).
Следовательно, точка \( C \) находится внутри угла \( \angle BAD \), а точки \( B \) и \( D \) лежат по разные стороны от прямой \( AC \).

2) Предположим, что четырехугольник ABCD — невыпуклый, и прямая \( BC \) пересекает сторону \( AD \). Тогда существует точка \( E \), где \( E = |BC| \cap |AD| \).
Точка \( C \) принадлежит отрезку \( BE \) и находится внутри угла \( \angle BAE \). Поскольку точка \( C \) также лежит внутри угла \( \angle BAD \), то точки \( B \) и \( D \) лежат по разные стороны от прямой \( AC \).

Следовательно, утверждение доказано.

Дано: ABCD — четырехугольник.
Доказать: точки \( B \) и \( D \) лежат по разные стороны от прямой \( AC \).

Решение:

1. Рассмотрим случай, когда четырехугольник ABCD является выпуклым.
Точки \( C \) и \( D \) лежат по одну сторону от прямой \( AB \), поскольку четырехугольник выпуклый, и обе эти точки принадлежат внутренней области четырехугольника.
Точки \( C \) и \( B \) лежат по одну сторону от прямой \( AD \), так как стороны \( AB \) и \( AD \) являются соседними сторонами выпуклого четырехугольника.
Таким образом, точка \( C \) находится внутри угла \( \angle BAD \), который образован сторонами \( AB \) и \( AD \).
Поскольку точка \( C \) лежит внутри угла \( \angle BAD \), то точки \( B \) и \( D \) обязательно оказываются по разные стороны от прямой \( AC \), которая проходит через вершины \( A \) и \( C \).

2. Рассмотрим случай, когда четырехугольник ABCD не является выпуклым.
В этом случае прямая \( BC \) может пересекать сторону \( AD \). Пусть точка пересечения этих прямых обозначена как \( E \), то есть \( E = |BC| \cap |AD| \).
Точка \( C \) принадлежит отрезку \( BE \), так как \( C \) — одна из вершин четырехугольника, а \( BE \) — часть диагонали \( BC \).
При этом точка \( C \) находится внутри угла \( \angle BAE \), который образован сторонами \( AB \) и \( AE \).
Поскольку точка \( C \) также лежит внутри угла \( \angle BAD \), то точки \( B \) и \( D \) будут лежать по разные стороны от прямой \( AC \), так как прямая \( AC \) разделяет внутреннюю область угла \( \angle BAD \).

Вывод: независимо от того, является ли четырехугольник ABCD выпуклым или невыпуклым, точки \( B \) и \( D \) всегда лежат по разные стороны от прямой \( AC \). Утверждение доказано.