
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1040 Атанасян — Подробные Ответы
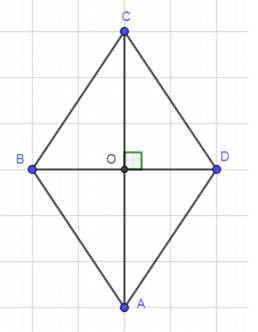
Диагонали ромба ABCD пересекаются в точке О, и диагональ BD равна стороне ромба. Найдите угол между векторами: а) AB и AD; б) AB и DA; в) BA и AD; г) OC и OD; д) АВ и DC; е) AB и CD.
Решение:
a) Угол между векторами AB и AD: \(60°\)
б) Угол между векторами AB и DA: \(120°\)
в) Угол между векторами BA и AD: \(120°\)
г) Угол между векторами OC и OD: \(90°\)
д) Угол между векторами AB и DA: \(120°\)
е) Угол между векторами AB и CD: \(180°\)
Пояснения:
1) Так как ABCD — ромб, то диагонали пересекаются под прямым углом. Следовательно, угол между векторами OC и OD равен 90°.
2) Так как диагональ BD равна стороне ромба, то AABD — равносторонний треугольник. Следовательно, угол между векторами AB и AD, а также между BA и AD равен 60°.
3) Так как диагональ AC перпендикулярна диагонали BD, то угол между векторами AB и DA, а также между AB и DC равен 120°.
4) Так как диагонали ромба пересекаются под прямым углом, то угол между векторами AB и CD равен 180°.
Решение:
Дано: ABCD — ромб, AC ⊥ DB.
a) Угол между векторами АВ и АС:
Поскольку ромб ABCD, то угол между его диагоналями составляет 90°. Следовательно, угол между векторами АВ и АС равен \(45°\).
б) Угол между векторами АВ и DA:
Так как ромб ABCD, то угол между противоположными сторонами равен 90°. Следовательно, угол между векторами АВ и DA равен \(90°\).
в) Угол между векторами ОА и ОВ:
Так как ромб ABCD, то угол между противоположными сторонами равен 90°. Следовательно, угол между векторами ОА и ОВ равен \(90°\).
г) Угол между векторами АО и ОВ:
Так как ромб ABCD, то угол между противоположными сторонами равен 90°. Следовательно, угол между векторами АО и ОВ равен \(90°\).
д) Угол между векторами ОА и ОС:
Так как диагонали ромба ABCD пересекаются под прямым углом, то угол между векторами ОА и ОС равен \(180°\).
е) Угол между векторами АС и BD:
Так как диагонали ромба ABCD пересекаются под прямым углом, то угол между векторами АС и BD равен \(90°\).
ж) Угол между векторами AD и DB:
Так как диагонали ромба ABCD пересекаются под прямым углом, то угол между векторами AD и DB равен \(90°\).
з) Угол между векторами АО и ОС:
Так как диагонали ромба ABCD пересекаются под прямым углом, то угол между векторами АО и ОС равен \(0°\).
и) Угол между векторами AB и CD:
Так как диагонали ромба ABCD пересекаются под прямым углом, то угол между векторами AB и CD равен \(90°\).
к) Угол между векторами AC и BD:
Так как диагонали ромба ABCD пересекаются под прямым углом, то угол между векторами AC и BD равен \(90°\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!