ГДЗ по Геометрии 9 класс Номер 1038 Атанасян — Подробные Ответы

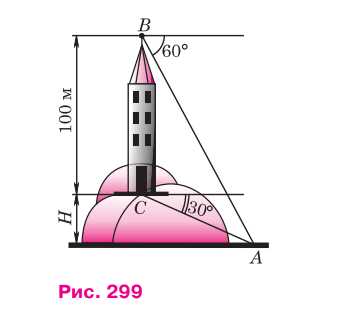
На горе находится башня, высота которой равна 100 м (рис. 299). Некоторый предмет А у подножия горы наблюда- ют сначала с вершины В башни под углом 60° к горизонту, а потом с её основания С под углом 30°. Найдите высоту Н горы.

Дано: BC = 100 м, ∠DCA = 30°, ∠ABE = 60°.

1) В прямоугольном треугольнике CBD: ∠CBD = 90° — 60° = 30°, ∠BDC = 90° — 30° = 60°, ∠CDA = 180° — 60° = 120° (как смежные).

2) В треугольнике ADC: ∠DAC = 180° — (120° + 30°) = 30° (по теореме о сумме углов в треугольнике), ∠DCA = ∠DAC = 30°, значит ADC — равнобедренный, CD = DA.

3) В прямоугольном треугольнике CAK: ∠CAK = 90° — 30° = 60°, ∠ACK = 90° — 60° = 30°.

4) В треугольнике ABC: ∠CBA = ∠BAC = 30°, значит ABC — равнобедренный, BC = CA = 100 м.

5) CK = 1/2 AC = 1/2 · 100 = 50 м (по свойству прямоугольного треугольника).

Ответ: 50 м.

Дано:
— Длина стороны BC прямоугольного треугольника ABC равна 100 м.
— Угол DCA равен 30°.
— Угол ABE равен 60°.

Решение:

1) Рассмотрим прямоугольный треугольник CBD.
— Угол CBD равен 90° — 60° = 30°.
— Угол BDC равен 90° — 30° = 60°.
— Угол CDA равен 180° — 60° = 120° (как смежный с углом ABE).

2) Рассмотрим треугольник ADC.
— Угол DAC равен 180° — (120° + 30°) = 30° (по теореме о сумме углов в треугольнике).
— Угол DCA равен 30°, значит треугольник ADC является равнобедренным, и CD = DA.

3) Рассмотрим прямоугольный треугольник CAK.
— Угол CAK равен 90° — 30° = 60°.
— Угол ACK равен 90° — 60° = 30°.

4) Рассмотрим треугольник ABC.
— Угол CBA равен 30°.
— Угол BAC равен 30°, значит треугольник ABC является равнобедренным, и BC = CA = 100 м.

5) Длина отрезка CK равна 1/2 длины отрезка AC, то есть 1/2 · 100 = 50 м (по свойству прямоугольного треугольника).

Ответ: Длина отрезка CK равна 50 м.