
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1035 Атанасян — Подробные Ответы
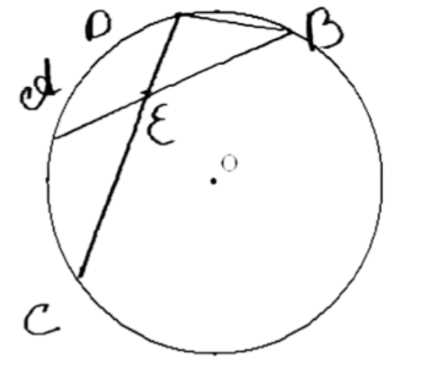
В окружности проведены хорды AB и CD, пересекающиеся в точке Е. Найдите острый угол между этими хордами, если АВ = 13 см, СЕ = 9 см, ED = 4 см и расстоя- ние между точками В и D равно 4/3 см.
Решение:
1) Находим длину отрезка EB: x(13-x) = 9·4 => x^2 — 13x + 36 = 0 => x1 = 4, x2 = 9. Так как EB = 13 — x, то EB = 13 — 9 = 4.
2) Треугольник AEB является равнобедренным, так как EB = 4. Используя теорему косинусов, находим угол DEB: (4√3)^2 = 4^2 + 9^2 — 72 cos(DEB) => cos(DEB) = 0,6806 => DEB = 47°7′.
3) Второй возможный угол BED равен 120°, так как треугольник AEB является равнобедренным.
Ответ: 120° или 47°7′.
Полное решение:
Дано:
— Окружность с центром в точке (0;г)
— Хорды AB и CD
— АВ = 13 см, СЕ = 9 см, ED = 4 см, BD = 4√3 см
— Требуется найти угол ∠BED
Решение:
1) Пусть длина отрезка АЕ равна х, тогда длина отрезка ЕВ равна 13 — х.
2) Согласно свойству пересекающихся хорд, произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды:
x(13 — x) = 9 · 4
x^2 — 13x + 36 = 0
x1 = 4, x2 = 9
Следовательно, EB = 13 — 9 = 4.
3) Треугольник AEB является равнобедренным, так как EB = 4.
Используя теорему косинусов, находим угол ∠DEB:
(4√3)^2 = 4^2 + 9^2 — 72 cos(∠DEB)
cos(∠DEB) = 0,6806
∠DEB = 47°7′
4) Второй возможный угол ∠BED равен 120°, так как треугольник AEB является равнобедренным.
Ответ: 120° или 47°7′.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!