
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1234 Атанасян — Подробные Ответы
Изобразите параллелепипед ABCDA1B1C1D1 и постройте: а) его сечения плоскостями ABС1 и DCB1, а также отрезок, по
которому эти сечения пересекаются; б) его сечение плоскостью, проходящей через ребро CC1 и точку пересечения диагоналей грани AA1D1D.
Изобразить: параллелепипед \(ABCDA_1B_1C_1D_1\);
Построить: сечение а) плоскостями \(ABC_1\) и \(DCB_1\) и отрезок, по которому они пересекаются; б) плоскостью, проходящей через ребро \(CC_1\) и точку пересечения диагоналей грани \(AA_1D_1D\).
Построение:
а)
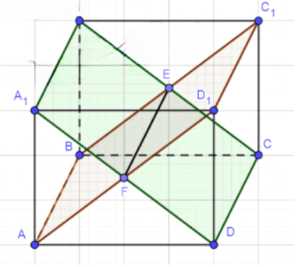
1) Проведем отрезок \(BC_1\);
2) Так как \(AA_1 \parallel DD_1 \parallel BB_1 \parallel CC_1\), через точку \(A\) построим отрезок, параллельный отрезку \(BC_1\) — это отрезок \(AD_1\);
3) \(ABC_1D_1\) — искомая плоскость;
4) Проведем отрезок \(CB_1\);
5) Так как \(AA_1 \parallel DD_1 \parallel BB_1 \parallel CC_1\), через точку \(D\) построим отрезок, параллельный отрезку \(CB_1\) — это отрезок \(DA_1\);
6) \(CDA_1B_1\) — искомая плоскость;
7) На пересечении отрезков \(B_1C\) и \(B_1C\) отметим точку \(E\), а на пересечении отрезков \(A_1D\) и \(AD_1\) точку \(F\);
8) Отрезок \(EF\) — искомый.
б)
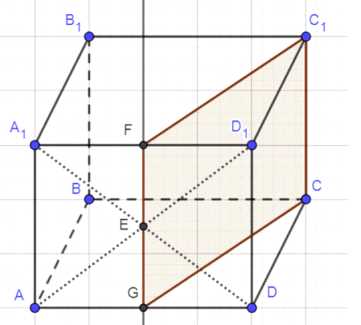
1) Отметим точку пересечения диагоналей грани \(AA_1D_1D\) — \(E\);
2) Так как \(AA_1 \parallel DD_1 \parallel BB_1 \parallel CC_1\), через точку \(E\) построим прямую, параллельную отрезку \(CC_1\);
3) Отметим точки \(F\) и \(G\) на пересечении данной прямой и ребер параллелепипеда;
4) Плоскость \(FGCC_1\) — искомая.
Для решения задачи построения сечений параллелепипеда \(ABCDA_1B_1C_1D_1\) рассмотрим два случая: а) сечение плоскостями \(ABC_1\) и \(DCB_1\); б) сечение плоскостью, проходящей через ребро \(CC_1\) и точку пересечения диагоналей грани \(AA_1D_1D\).
Построение а)
1. Проведем отрезок \(BC_1\): Соединяем вершины \(B\) и \(C_1\), получая отрезок \(BC_1\).
2. Построим отрезок \(AD_1\): Поскольку \(AA_1 \parallel DD_1 \parallel BB_1 \parallel CC_1\), через точку \(A\) строим отрезок, параллельный \(BC_1\). Это будет отрезок \(AD_1\).
3. Определяем плоскость \(ABC_1D_1\): Плоскость, проходящая через точки \(A\), \(B\), \(C_1\), и \(D_1\), является искомой.
4. Проведем отрезок \(CB_1\): Соединяем вершины \(C\) и \(B_1\), получая отрезок \(CB_1\).
5. Построим отрезок \(DA_1\): Так как \(AA_1 \parallel DD_1 \parallel BB_1 \parallel CC_1\), через точку \(D\) строим отрезок, параллельный \(CB_1\). Это будет отрезок \(DA_1\).
6. Определяем плоскость \(CDA_1B_1\): Плоскость, проходящая через точки \(C\), \(D\), \(A_1\), и \(B_1\), является искомой.
7. Находим точки пересечения: На пересечении отрезков \(B_1C\) и \(BC_1\) отмечаем точку \(E\). На пересечении отрезков \(A_1D\) и \(AD_1\) отмечаем точку \(F\).
8. Определяем отрезок \(EF\): Отрезок \(EF\) — это линия пересечения двух плоскостей \(ABC_1D_1\) и \(CDA_1B_1\).
Построение б)
1. Определим точку пересечения диагоналей грани \(AA_1D_1D\): Точка \(E\) является точкой пересечения диагоналей \(AA_1\) и \(D_1D\).
2. Построим прямую через точку \(E\): Поскольку \(AA_1 \parallel DD_1 \parallel BB_1 \parallel CC_1\), через точку \(E\) проводим прямую, параллельную отрезку \(CC_1\).
3. Определим точки \(F\) и \(G\): Отмечаем точки \(F\) и \(G\) на пересечении данной прямой с ребрами параллелепипеда.
4. Определяем плоскость \(FGCC_1\): Плоскость, проходящая через точки \(F\), \(G\), \(C\), и \(C_1\), является искомой.
Эти шаги позволяют построить сечения параллелепипеда и определить линии пересечения плоскостей.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!