
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1294 Атанасян — Подробные Ответы
Докажите, что две трапеции равны, если основания и боковые стороны одной трапеции соответственно равны основаниям и боковым сторонам другой.
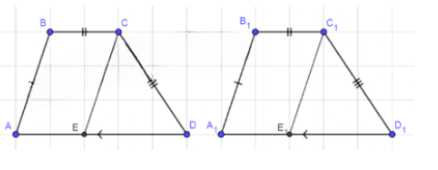
1. Дано: \(ABCD\), \(A_1B_1C_1D_1\) — трапеции, \(AD \parallel BC\), \(AD > BC\), \(A_1D_1 \parallel B_1C_1\), \(A_1D_1 > B_1C_1\); \(AB = A_1B_1\), \(BC = B_1C_1\), \(CD = C_1D_1\), \(AD = A_1D_1\); Доказать: \(ABCD = A_1B_1C_1D_1\);
2. Доказательство:
— Проведем отрезки \(CE \parallel AB\), \(E \in AD\), \(C_1E_1 \parallel A_1B_1\), \(E_1 \in A_1D_1\);
— По построению \(ABCE\) и \(A_1B_1C_1E_1\) — параллелограммы: \(AB = CE = A_1B_1 = C_1E_1\), \(BC = AE = B_1C_1 = A_1E_1\), \(CE = C_1E_1\), \(CD = C_1D_1\) (3-й признак) \(\Rightarrow \triangle ECD = \triangle E_1C_1D_1\), \(ED = AD — AE = A_1D_1 — A_1E_1 = E_1D_1\).
— Существует наложение \(f: \triangle ECD \rightarrow \triangle E_1C_1D_1\).
3. Совместим эти треугольники. Для двух пар вершин получим:
— Тогда совместятся отрезки \(AD\) и \(A_1D_1\) как продолжения сторон \(ED\) и \(E_1D_1\). Совместятся точки \(A\) и \(A_1\).
4. Через точку \(A\) можно провести только одну прямую, параллельную \(CE\), через точку \(C\) — только одну прямую, параллельную \(AD\). Точка пересечения \(B = AB \cap CB\).
5. Аналогично, во второй трапеции. Значит, совместятся точки \(B\) и \(B_1\). При наложении совместились все четыре вершины \(\Rightarrow ABCD \cong A_1B_1C_1D_1 \Rightarrow ABCD = A_1B_1C_1D_1\). Что и требовалось доказать.
Дано две трапеции \(ABCD\) и \(A_1B_1C_1D_1\) с параллельными основаниями \(AD \parallel BC\) и \(A_1D_1 \parallel B_1C_1\), причем \(AD > BC\) и \(A_1D_1 > B_1C_1\). Известно, что соответствующие стороны равны: \(AB = A_1B_1\), \(BC = B_1C_1\), \(CD = C_1D_1\), \(AD = A_1D_1\). Требуется доказать, что трапеции \(ABCD\) и \(A_1B_1C_1D_1\) равны.
Проведем построение: из точек \(C\) и \(C_1\) опустим перпендикуляры \(CE\) и \(C_1E_1\) на стороны \(AD\) и \(A_1D_1\) соответственно, так чтобы \(CE \parallel AB\) и \(C_1E_1 \parallel A_1B_1\). Поскольку \(AB \parallel CE\) и \(A_1B_1 \parallel C_1E_1\), четырехугольники \(ABCE\) и \(A_1B_1C_1E_1\) являются параллелограммами. Из свойств параллелограмма следует, что \(AB = CE\) и \(A_1B_1 = C_1E_1\), а также \(BC = AE\) и \(B_1C_1 = A_1E_1\).
Так как \(AB = A_1B_1\), то \(CE = C_1E_1\). Также по условию \(CD = C_1D_1\). Рассмотрим треугольники \(ECD\) и \(E_1C_1D_1\): у них равны две стороны \(CE = C_1E_1\), \(CD = C_1D_1\) и угол между ними (так как \(CE \parallel AB\) и \(C_1E_1 \parallel A_1B_1\), а \(AB\) и \(A_1B_1\) равны и одинаково ориентированы). Следовательно, по второму признаку равенства треугольников \(\triangle ECD = \triangle E_1C_1D_1\).
Из равенства треугольников следует, что \(ED = E_1D_1\). Поскольку \(ED = AD — AE\) и \(E_1D_1 = A_1D_1 — A_1E_1\), а \(AE = BC = B_1C_1 = A_1E_1\), то \(AD — BC = A_1D_1 — B_1C_1\). Но \(AD = A_1D_1\) по условию, значит, \(BC = B_1C_1\) также выполняется.
Теперь применим наложение (движение плоскости), которое переводит \(\triangle ECD\) в \(\triangle E_1C_1D_1\). При этом точка \(E\) совместится с \(E_1\), точка \(C\) — с \(C_1\), а точка \(D\) — с \(D_1\). Так как \(AD\) и \(A_1D_1\) являются продолжениями сторон \(ED\) и \(E_1D_1\) соответственно, они также совместятся.
Точка \(A\) лежит на прямой \(AD\) и находится на расстоянии \(AE = BC = B_1C_1 = A_1E_1\) от точки \(E\). Поскольку \(E\) совместилась с \(E_1\), а \(AD\) с \(A_1D_1\), точка \(A\) совпадет с \(A_1\).
Через точку \(A\) можно провести единственную прямую, параллельную \(CE\) (это \(AB\)), а через точку \(C\) — единственную прямую, параллельную \(AD\) (это \(CB\)). Точка пересечения этих прямых — \(B\). Аналогично, во второй трапеции точка \(B_1\) определяется пересечением \(A_1B_1 \parallel C_1E_1\) и \(C_1B_1 \parallel A_1D_1\).
Таким образом, при наложении совпадут все четыре вершины: \(A\) с \(A_1\), \(B\) с \(B_1\), \(C\) с \(C_1\), \(D\) с \(D_1\). Следовательно, трапеции \(ABCD\) и \(A_1B_1C_1D_1\) полностью совпадают при наложении, а значит, они равны. Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!