
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 959 Атанасян — Подробные Ответы
Начертите окружность, заданную уравнением:
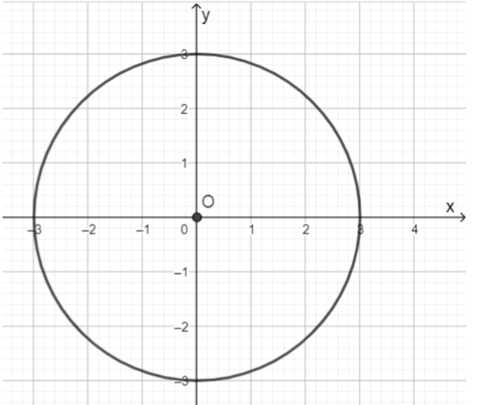
a) \(x^2+y^2=9\);
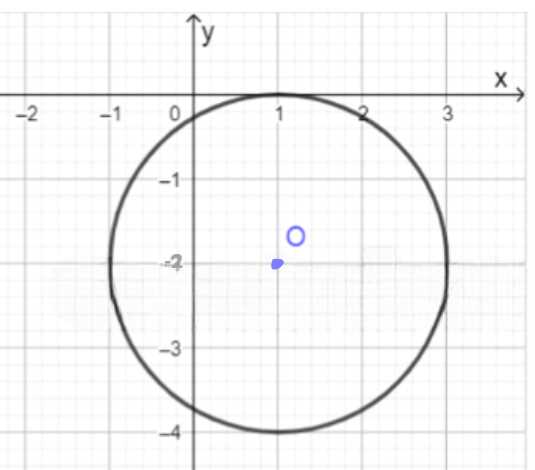
б) \((x-1)^2+(y+2)^2=4\);
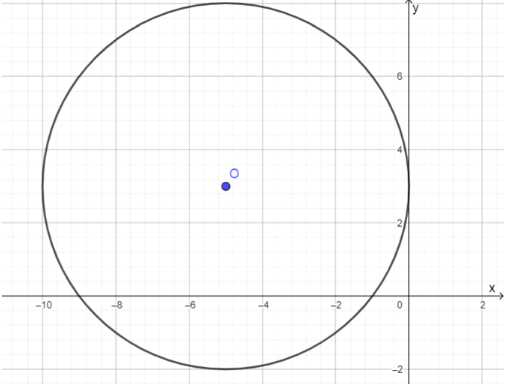
в) \((x+5)^2+(y-3)^2=25\);
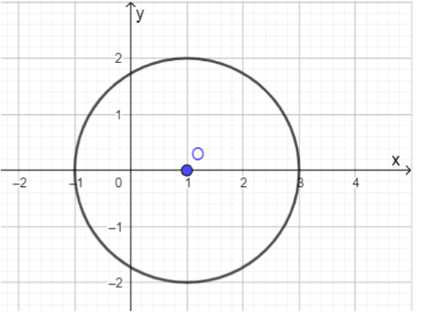
г) \((x — 1)^2 + y^2 = 4\);
д) \(x^2 + (y + 2)^2=2\).
1. Уравнение: \(x^2 + y^2 = 9\)
Центр: \((0, 0)\)
Радиус: \(3\)
2. Уравнение: \((x — 1)^2 + (y + 2)^2 = 4\)
Центр: \((1, -2)\)
Радиус: \(2\)
3. Уравнение: \((x + 5)^2 + (y — 3)^2 = 25\)
Центр: \((-5, 3)\)
Радиус: \(5\)
4. Уравнение: \((x — 1)^2 + y^2 = 4\)
Центр: \((1, 0)\)
Радиус: \(2\)
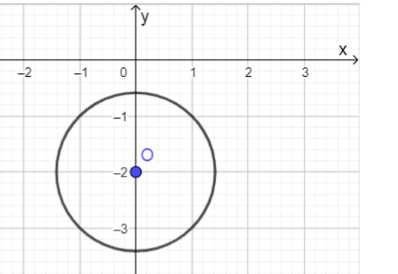
5. Уравнение: \(x^2 + (y + 2)^2 = 2\)
Центр: \((0, -2)\)
Радиус: \(\sqrt{2} \approx 1.41\)
Для графического изображения окружностей используйте заданные центры и радиусы.
Давайте подробно разберем каждое уравнение окружности, чтобы определить его центр и радиус.
1. Уравнение: \(x^2 + y^2 = 9\)
Это уравнение имеет вид \(x^2 + y^2 = r^2\), где \(r\) — радиус окружности. Здесь центр окружности находится в точке \((0, 0)\), а радиус \(r = \sqrt{9} = 3\).
2. Уравнение: \((x — 1)^2 + (y + 2)^2 = 4\)
Это уравнение имеет вид \((x — h)^2 + (y — k)^2 = r^2\), где \((h, k)\) — координаты центра окружности. Здесь \(h = 1\), \(k = -2\), а радиус \(r = \sqrt{4} = 2\). Таким образом, центр окружности \((1, -2)\), радиус \(2\).
3. Уравнение: \((x + 5)^2 + (y — 3)^2 = 25\)
Это уравнение также имеет вид \((x — h)^2 + (y — k)^2 = r^2\). Здесь \(h = -5\), \(k = 3\), а радиус \(r = \sqrt{25} = 5\). Таким образом, центр окружности \((-5, 3)\), радиус \(5\).
4. Уравнение: \((x — 1)^2 + y^2 = 4\)
Здесь уравнение имеет вид \((x — h)^2 + (y — k)^2 = r^2\), где \(h = 1\), \(k = 0\), а радиус \(r = \sqrt{4} = 2\). Таким образом, центр окружности \((1, 0)\), радиус \(2\).
5. Уравнение: \(x^2 + (y + 2)^2 = 2\)
Это уравнение имеет вид \(x^2 + (y — k)^2 = r^2\), где \(h = 0\), \(k = -2\), а радиус \(r = \sqrt{2} \approx 1.41\). Таким образом, центр окружности \((0, -2)\), радиус приближенно равен \(1.41\).
Таким образом, для каждого уравнения мы определили центр и радиус окружности. Все дробные ответы представлены в виде десятичных дробей.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!