ГДЗ по Геометрии 9 класс Номер 947 Атанасян — Подробные Ответы

Докажите, что треугольник АВС равнобедренный, и найдите его площадь, если вершины треугольника имеют координаты:
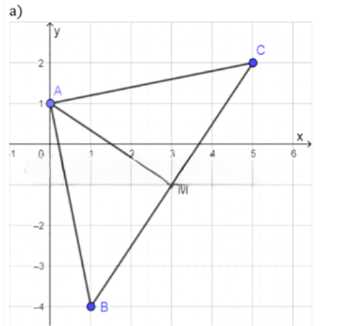
а) A (0; 1), B (1; -4), C (5; 2);
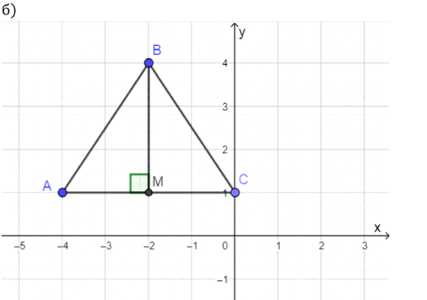
б) A (-4; 1), B (-2; 4), C (0; 1).

а) Треугольник \(ABC\) с вершинами \(A(0; 1)\), \(B(1; -4)\), \(C(5; 2)\)

1. Найдем длины сторон:

\(
AB = \sqrt{(1 — 0)^2 + (-4 — 1)^2} = \sqrt{1 + 25} = \sqrt{26}
\)

\(
BC = \sqrt{(5 — 1)^2 + (2 + 4)^2} = \sqrt{16 + 36} = \sqrt{52} = 2\sqrt{13}
\)

\(
AC = \sqrt{(5 — 0)^2 + (2 — 1)^2} = \sqrt{25 + 1} = \sqrt{26}
\)

2. Так как \(AB = AC\), треугольник равнобедренный.

3. Найдем площадь:

\(
AM = \sqrt{(3 — 0)^2 + (-1 — 1)^2} = \sqrt{9 + 4} = \sqrt{13}
\)

\(
S_{ABC} = \frac{1}{2} \cdot AM \cdot BC = \frac{1}{2} \cdot \sqrt{13} \cdot 2\sqrt{13} = 13
\)

б) Треугольник \(ABC\) с вершинами \(A(-4; 1)\), \(B(-2; 4)\), \(C(0; 1)\)

1. Найдем длины сторон:

\(
AB = \sqrt{(-2 + 4)^2 + (4 — 1)^2} = \sqrt{4 + 9} = \sqrt{13}
\)

\(
BC = \sqrt{(0 + 2)^2 + (1 — 4)^2} = \sqrt{4 + 9} = \sqrt{13}
\)

\(
AC = \sqrt{(0 + 4)^2 + (1 — 1)^2} = \sqrt{16 + 0} = 4
\)

2. Так как \(AB = BC\), треугольник равнобедренный.

3. Найдем площадь:

\(
BM = \sqrt{(-2 + 2)^2 + (1 — 4)^2} = \sqrt{0 + 9} = 3
\)

\(
S_{ABC} = \frac{1}{2} \cdot BM \cdot AC = \frac{1}{2} \cdot 3 \cdot 4 = 6
\)

Ответы: а) 13; б) 6.

Решение задачи

а) Треугольник \(ABC\) с вершинами \(A(0; 1)\), \(B(1; -4)\), \(C(5; 2)\)

1. Найдем длины сторон треугольника. Для этого используем формулу расстояния между двумя точками:

\(
AB = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}
\)

\(
AB = \sqrt{(1 — 0)^2 + (-4 — 1)^2} = \sqrt{1 + 25} = \sqrt{26}
\)

\(
BC = \sqrt{(5 — 1)^2 + (2 + 4)^2} = \sqrt{16 + 36} = \sqrt{52} = 2\sqrt{13}
\)

\(
AC = \sqrt{(5 — 0)^2 + (2 — 1)^2} = \sqrt{25 + 1} = \sqrt{26}
\)

2. Так как \(AB = AC\), треугольник равнобедренный, что и требовалось доказать.

3. Найдем высоту \(AM\), используя формулу расстояния:

\(
AM = \sqrt{(x_M — x_A)^2 + (y_M — y_A)^2}
\)

Найдем координаты точки \(M\), которая является серединой отрезка \(BC\):

\(
x_M = \frac{x_B + x_C}{2} = \frac{1 + 5}{2} = 3
\)

\(
y_M = \frac{y_B + y_C}{2} = \frac{-4 + 2}{2} = -1
\)

Теперь найдем \(AM\):

\(
AM = \sqrt{(3 — 0)^2 + (-1 — 1)^2} = \sqrt{9 + 4} = \sqrt{13}
\)

4. Найдем площадь треугольника \(ABC\) по формуле площади через высоту:

\(
S_{ABC} = \frac{1}{2} \cdot AM \cdot BC = \frac{1}{2} \cdot \sqrt{13} \cdot 2\sqrt{13} = 13
\)

б) Треугольник \(ABC\) с вершинами \(A(-4; 1)\), \(B(-2; 4)\), \(C(0; 1)\)

1. Найдем длины сторон треугольника:

\(
AB = \sqrt{(-2 + 4)^2 + (4 — 1)^2} = \sqrt{4 + 9} = \sqrt{13}
\)

\(
BC = \sqrt{(0 + 2)^2 + (1 — 4)^2} = \sqrt{4 + 9} = \sqrt{13}
\)

\(
AC = \sqrt{(0 + 4)^2 + (1 — 1)^2} = \sqrt{16 + 0} = 4
\)

2. Так как \(AB = BC\), треугольник равнобедренный, что и требовалось доказать.

3. Найдем высоту \(BM\), используя формулу расстояния:

Найдем координаты точки \(M\), которая является серединой отрезка \(AC\):

\(
x_M = \frac{x_A + x_C}{2} = \frac{-4 + 0}{2} = -2
\)

\(
y_M = \frac{y_A + y_C}{2} = \frac{1 + 1}{2} = 1
\)

Теперь найдем \(BM\):

\(
BM = \sqrt{(-2 + 2)^2 + (1 — 4)^2} = \sqrt{0 + 9} = 3
\)

4. Найдем площадь треугольника \(ABC\) по формуле площади через высоту:

\(
S_{ABC} = \frac{1}{2} \cdot BM \cdot AC = \frac{1}{2} \cdot 3 \cdot 4 = 6
\)

Ответы: а) 13; б) 6.