ГДЗ по Геометрии 9 класс Номер 915 Атанасян — Подробные Ответы

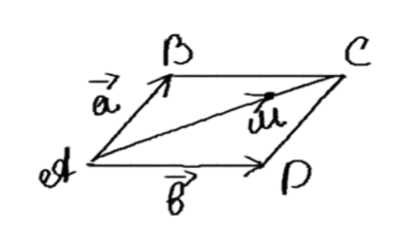
915 Точка М лежит на диагонали АС параллелограмма ABCD, причём АМ : МС = 4: 1. Разложите вектор АМ по векторам \(\overrightarrow{a} = \overrightarrow{AB}\) и \(\overrightarrow{b} = \overrightarrow{AD}\).

Для решения задачи используем следующее:

1. Точка \( M \) делит диагональ \( AC \) в отношении \( 4:1 \), значит, вектор \( \overrightarrow{AM} = \frac{4}{5} \overrightarrow{AC} \).

2. По правилу параллелограмма, \(\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD}\).

3. Подставляем: \(\overrightarrow{AM} = \frac{4}{5}(\overrightarrow{AB} + \overrightarrow{AD})\).

Таким образом, вектор \(\overrightarrow{AM}\) можно разложить по векторам \(\overrightarrow{a} = \overrightarrow{AB}\) и \(\overrightarrow{b} = \overrightarrow{AD}\) как:

\(
\overrightarrow{AM} = \frac{4}{5} \overrightarrow{a} + \frac{4}{5} \overrightarrow{b}
\)

Давайте подробно разберем решение задачи.

1. Определение отношения: Точка \( M \) делит диагональ \( AC \) в отношении \( AM:MC = 4:1 \). Это значит, что точка \( M \) находится на \(\frac{4}{5}\) пути от \( A \) до \( C \).

2. Векторное представление: Нам нужно разложить вектор \( \overrightarrow{AM} \) по векторам \(\overrightarrow{a} = \overrightarrow{AB}\) и \(\overrightarrow{b} = \overrightarrow{AD}\).

3. Диагональ параллелограмма: По свойству параллелограмма, диагональ \( AC \) выражается через векторы как:
\(
\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD}
\)

4. Выражение для \( \overrightarrow{AM} \): Поскольку \( M \) делит \( AC \) в отношении \( 4:1 \), то:
\(
\overrightarrow{AM} = \frac{4}{5} \overrightarrow{AC}
\)

5. Подстановка выражения для \( \overrightarrow{AC} \): Подставим выражение для \( \overrightarrow{AC} \) в формулу для \( \overrightarrow{AM} \):
\(
\overrightarrow{AM} = \frac{4}{5} (\overrightarrow{AB} + \overrightarrow{AD})
\)

6. Разложение по векторам \( \overrightarrow{a} \) и \( \overrightarrow{b} \): Раскроем скобки:
\(
\overrightarrow{AM} = \frac{4}{5} \overrightarrow{AB} + \frac{4}{5} \overrightarrow{AD}
\)

7. Итоговое выражение: Таким образом, вектор \( \overrightarrow{AM} \) можно разложить по векторам \(\overrightarrow{a}\) и \(\overrightarrow{b}\) следующим образом:
\(
\overrightarrow{AM} = \frac{4}{5} \overrightarrow{a} + \frac{4}{5} \overrightarrow{b}
\)

Это полное решение задачи, где вектор \( \overrightarrow{AM} \) выражен через заданные векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\).