ГДЗ по Геометрии 9 класс Номер 887 Атанасян — Подробные Ответы

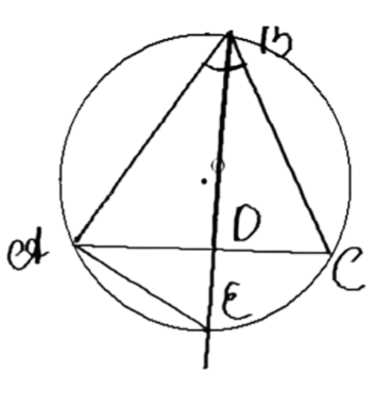
Отрезок \( BD \) — биссектриса треугольника \( ABC \). Докажите, что
\(
BD^2 = AB \cdot BC — AD \cdot DC.
\)

Рассмотрим задачу:

Дано: \( \triangle ABC \), \( BD \) — биссектриса.
Требуется доказать: \( BD^2 = AB \cdot BC — AD \cdot DC \).

Решение:
1. Построим окружность, описанную вокруг \( \triangle ABC \). Обозначим её центр \( O \) и радиус \( R \).

2. Продолжим луч \( BD \) и найдём точку пересечения \( K \), где \( K = (O; R) \cap BD \).
3. Рассмотрим треугольники \( \triangle BDC \) и \( \triangle BAK \). Углы \( \angle ABK \) и \( \angle DBC \) равны, так как \( BD \) — биссектриса. Также \( \angle AKB = \angle ABC \). Следовательно, треугольники \( \triangle BAK \sim \triangle BDC \) по двум углам.

Из подобия треугольников следует:
\(
\frac{AB}{BD} = \frac{BK}{BC}.
\)

4. Выразим произведение \( BD \cdot BK \):
\(
BD \cdot BK = AB \cdot BC.
\)
Подставим \( BK = BD + DK \):
\(
BD \cdot (BD + DK) = AB \cdot BC.
\)
Раскроем скобки:
\(
BD^2 + BD \cdot DK = AB \cdot BC.
\)
Выразим \( BD^2 \):
\(
BD^2 = AB \cdot BC — BD \cdot DK.
\)

5. По свойству пересекающихся хорд:
\(
BD \cdot DK = AD \cdot DC.
\)
Подставим это значение:
\(
BD^2 = AB \cdot BC — AD \cdot DC.
\)

Таким образом, требуемое равенство доказано.

Дано: \( \triangle ABC \), \( BD \) — биссектриса.
Требуется доказать: \( BD^2 = AB \cdot BC — AD \cdot DC \).

Решение:

1. Построим окружность, описанную вокруг \( \triangle ABC \). Обозначим её центр \( O \) и радиус \( R \). Точки \( A, B, C \) лежат на окружности. Продолжим луч \( BD \) и найдём точку пересечения \( K \), где \( K = (O; R) \cap BD \). Таким образом, точка \( K \) находится на окружности и лежит на продолжении биссектрисы \( BD \).

2. Рассмотрим треугольники \( \triangle BDC \) и \( \triangle BAK \). Углы \( \angle ABK \) и \( \angle DBC \) равны, так как \( BD \) — биссектриса, которая делит угол \( \angle ABC \) пополам. Также углы \( \angle AKB \) и \( \angle ABC \) равны, поскольку они опираются на одну и ту же дугу \( AC \) окружности. Следовательно, треугольники \( \triangle BAK \) и \( \triangle BDC \) подобны по двум углам.

3. Из подобия треугольников \( \triangle BAK \sim \triangle BDC \) можно записать отношение сторон:
\(
\frac{AB}{BD} = \frac{BK}{BC}.
\)
Отсюда выразим произведение \( BD \cdot BK \):
\(
BD \cdot BK = AB \cdot BC.
\)

4. Подставим значение \( BK \) через \( BD \) и \( DK \):
\(
BK = BD + DK.
\)
Тогда:
\(
BD \cdot BK = BD \cdot (BD + DK) = AB \cdot BC.
\)
Раскроем скобки:
\(
BD^2 + BD \cdot DK = AB \cdot BC.
\)
Выразим \( BD^2 \):
\(
BD^2 = AB \cdot BC — BD \cdot DK.
\)

5. По свойству пересекающихся хорд в окружности:
Если две хорды пересекаются в точке \( D \), то произведение отрезков одной хорды равно произведению отрезков другой хорды. В данном случае:
\(
BD \cdot DK = AD \cdot DC.
\)
Подставим это значение в выражение для \( BD^2 \):
\(
BD^2 = AB \cdot BC — AD \cdot DC.
\)

Таким образом, доказательство завершено. Равенство \( BD^2 = AB \cdot BC — AD \cdot DC \) выполнено.