ГДЗ по Геометрии 9 класс Номер 877 Атанасян — Подробные Ответы

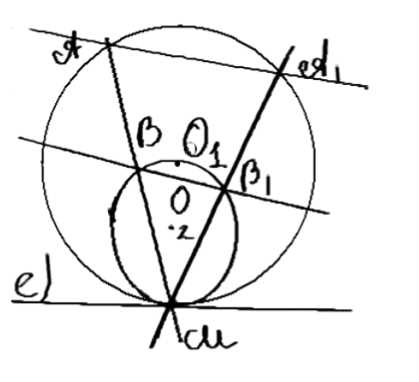
Две окружности имеют единственную общую точку \( M \). Через эту точку проведены две секущие, пересекающие одну окружность в точках \( A \) и \( A_1 \), а другую — в точках \( B \) и \( B_1 \). Докажите, что \( AA_1 \parallel BB_1 \). 

Рассмотрим доказательство задачи.

Дано: точки \(O_1\) и \(O_2\) — центры окружностей радиусов \(r\) и \(R\), которые касаются друг друга в точке \(M\). Секущие \(AB_1\), \(A_1B\) пересекают окружности. Требуется доказать, что \(AA_1 \parallel BB_1\).

Рассмотрим два случая: внешнее касание и внутреннее касание.

1. Для внешнего касания:

Проведем касательную \(CD\).
Углы, образованные касательной \(CD\) и секущей \(A_1B\):
\(
\angle AMD = \angle A_1M, \quad \angle CMB = \angle MB
\)
Так как вертикальные углы равны, то:
\(
\angle A_1M = \angle MB
\)
Следовательно:
\(
\angle A_1AM = \angle B_1BM
\)
Так как накрест лежащие углы равны, то \(AA_1 \parallel BB_1\).

2. Для внутреннего касания:
Углы, образованные касательной \(CD\) и секущей \(A_1B\):
\(
\angle AMD = \angle A_1M, \quad \angle B_1MD = \angle BM
\)
Так как вертикальные углы равны, то:
\(
\angle A_1M = \angle B_1M
\)
Следовательно:

\(
\angle AA_1M = \angle BB_1M
\)
Так как накрест лежащие углы равны, то \(AA_1 \parallel BB_1\).

Таким образом, доказательство завершено.

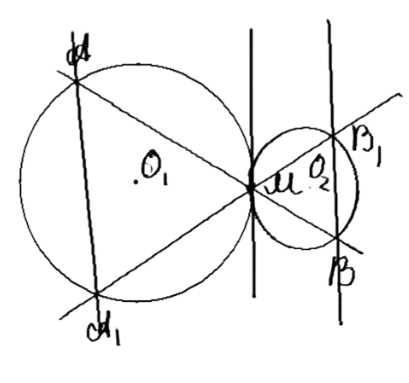
Дано: точки \(O_1\) и \(O_2\) — центры окружностей радиусов \(r\) и \(R\), которые касаются друг друга в точке \(M\). Секущие \(AB_1\), \(A_1B\) пересекают окружности. Требуется доказать, что \(AA_1 \parallel BB_1\).

Рассмотрим два случая: внешнее касание и внутреннее касание.

Для внешнего касания:

1. Проведем касательную \(CD\) к обеим окружностям.

2. Рассмотрим углы, которые образуют касательная \(CD\) и секущая \(A_1B\):
\(
\angle AMD = \angle A_1M, \quad \angle CMB = \angle MB
\)
Эти углы равны, так как они вертикальные.

3. Следовательно, равенство вертикальных углов приводит к следующему соотношению:
\(
\angle A_1M = \angle MB
\)

4. Теперь рассмотрим углы \(\angle A_1AM\) и \(\angle B_1BM\), которые образуются на пересечении секущей с окружностями.
Так как \(\angle A_1M = \angle MB\), то:
\(
\angle A_1AM = \angle B_1BM
\)

5. Углы \(\angle A_1AM\) и \(\angle B_1BM\) являются накрест лежащими. По свойству накрест лежащих углов, если они равны, то прямые \(AA_1\) и \(BB_1\) параллельны. Таким образом:
\(
AA_1 \parallel BB_1
\)

Для внутреннего касания:

1. Рассмотрим углы, которые образуют касательная \(CD\) и секущая \(A_1B\):
\(
\angle AMD = \angle A_1M, \quad \angle B_1MD = \angle BM
\)
Эти углы равны, так как они вертикальные.

2. Следовательно, равенство вертикальных углов приводит к следующему соотношению:
\(
\angle A_1M = \angle B_1M
\)

3. Теперь рассмотрим углы \(\angle AA_1M\) и \(\angle BB_1M\), которые образуются на пересечении секущей с окружностями.
Так как \(\angle A_1M = \angle B_1M\), то:
\(
\angle AA_1M = \angle BB_1M
\)

4. Углы \(\angle AA_1M\) и \(\angle BB_1M\) являются накрест лежащими. По свойству накрест лежащих углов, если они равны, то прямые \(AA_1\) и \(BB_1\) параллельны. Таким образом:
\(
AA_1 \parallel BB_1
\)

Вывод: в обоих случаях доказано, что \(AA_1 \parallel BB_1\).