ГДЗ по Геометрии 9 класс Номер 847 Атанасян — Подробные Ответы

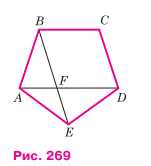
На рисунке 269 изображён правильный пятиугольник \( ABCDE \), т.е. выпуклый пятиугольник, у которого все углы равны и все стороны равны.

Докажите, что:  

а) \( \triangle AED \sim \triangle AFE \);  

б) \( \frac{DA}{DF} = \frac{DF}{AF} \).  

Дано: ABCD — правильный пятиугольник; F — точка пересечения диагоналей AD и BE.

Доказать:
а) ΔAED ~ ΔAFE;
б) \(\frac{DA}{DF} = \frac{DF}{AF}\).

Решение:
1. Сумма углов пятиугольника:
\(
S_5 = (5 — 2) \cdot 180 = 540^\circ.
\)

2. Величина каждого угла пятиугольника:
\(
\alpha = \frac{540}{5} = 108^\circ.
\)

3. Треугольник \(\triangle AED\) равнобедренный (\(AE = ED\)), углы при основании \(AD\) равны:
\(
\angle AED = 108^\circ,\quad \angle DAE = \angle ADE = \frac{180 — 108}{2} = 36^\circ.
\)

4. Рассмотрим треугольник \(\triangle AFE\):
\(
\angle FAE = \angle DAE = 36^\circ,\quad \angle FEA = \angle BEA = 36^\circ.
\)
По первому признаку подобия (\(2\) угла), \(\triangle AED \sim \triangle AFE\).

5. Из подобия треугольников:
\(
\frac{DA}{AE} = \frac{DF}{AF},
\)
следовательно:
\(
DA \cdot AF = AE^2.
\)

6. Рассмотрим треугольник \(\triangle ADF\):
\(
\angle DFE = 180^\circ — \angle AFE = 180^\circ — 108^\circ = 72^\circ,\quad \angle FDE = 36^\circ.
\)
Значит:
\(
\angle DEF = 180^\circ — (72^\circ + 36^\circ) = 72^\circ = \angle DFE.
\)
Таким образом, треугольник \(\triangle DEF\) равнобедренный (\(DF = DE\)).

7. Так как \(DE\) — сторона пятиугольника, то \(DE = AE\).
Отсюда:
\(
DF = AE.
\)
Подставляем в формулу подобия:
\(
DA \cdot AF = DF^2.
\)
Что и требовалось доказать.

Дано: ABCD — правильный пятиугольник, F — точка пересечения диагоналей AD и BE.

Доказать:
а) ΔAED ~ ΔAFE;
б) \(\frac{DA}{DF} = \frac{DF}{AF}\).

Решение:
1. Найдем сумму углов правильного пятиугольника:
\(
S_5 = (5 — 2) \cdot 180 = 540^\circ.
\)

2. Найдем величину каждого угла пятиугольника:
\(
\alpha = \frac{540}{5} = 108^\circ.
\)

3. Рассмотрим треугольник \(\triangle AED\). Поскольку пятиугольник правильный, его стороны равны, а диагонали пересекаются под определенными углами. Треугольник \(\triangle AED\) равнобедренный (\(AE = ED\)), следовательно, углы при основании \(AD\) равны.
\(
\angle AED = 108^\circ,\quad \angle DAE = \angle ADE = \frac{180 — 108}{2} = 36^\circ.
\)

4. Рассмотрим треугольник \(\triangle AFE\). В нем угол \(\angle FAE = \angle DAE = 36^\circ\), так как точка F принадлежит диагонали AD. Угол \(\angle FEA = \angle BEA = 36^\circ\), так как точка F принадлежит диагонали BE. Таким образом, два угла треугольников \(\triangle AED\) и \(\triangle AFE\) равны.
По первому признаку подобия треугольников имеем:
\(
\triangle AED \sim \triangle AFE.
\)

5. Из подобия треугольников следует, что их стороны пропорциональны:
\(
\frac{DA}{AE} = \frac{DF}{AF}.
\)
Умножая пропорцию на \(AE \cdot AF\), получаем:
\(
DA \cdot AF = AE^2.
\)

6. Рассмотрим треугольник \(\triangle ADF\). Найдем углы этого треугольника.
Угол \(\angle DFE = 180^\circ — \angle AFE = 180^\circ — 108^\circ = 72^\circ.\)
Угол \(\angle FDE = 36^\circ\), так как он равен углу \(\angle FAE\).
Остался третий угол:
\(
\angle DEF = 180^\circ — (\angle DFE + \angle FDE) = 180^\circ — (72^\circ + 36^\circ) = 72^\circ.
\)
Таким образом, треугольник \(\triangle DEF\) равнобедренный (\(DF = DE\)).

7. Поскольку \(DE\) — сторона правильного пятиугольника, то \(DE = AE\). Следовательно, \(DF = AE\).

8. Подставим это в ранее полученное равенство:
\(
DA \cdot AF = DF^2.
\)
Таким образом, доказано, что:
\(
\frac{DA}{DF} = \frac{DF}{AF}.
\)

Ответ:
а) \(\triangle AED \sim \triangle AFE\);
б) \(\frac{DA}{DF} = \frac{DF}{AF}\).