ГДЗ по Геометрии 9 класс Номер 839 Атанасян — Подробные Ответы

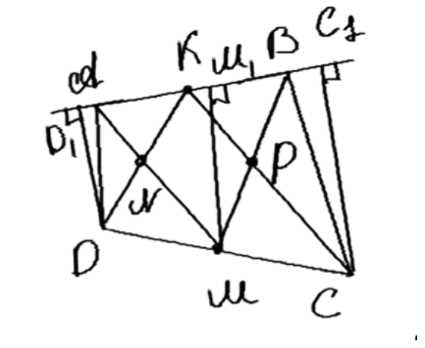
Середины \( K \) и \( M \) сторон \( AB \) и \( DC \) выпуклого четырёхугольника \( ABCD \) соединены отрезками \( KD \), \( KC \), \( MA \) и \( MB \) соответственно с его вершинами. Докажите, что площадь четырёхугольника, заключённого между этими отрезками, равна сумме площадей двух треугольников, прилежащих к сторонам \( AD \) и \( BC \). 

Рассмотрим выпуклый четырехугольник \(ABCD\), где точки \(K\), \(E\), \(M\), \(F\) делят стороны \(AB\), \(BC\), \(CD\), \(DA\) на равные части. Пусть \(AK = KB = a\), \(CM = MD = b\). Требуется доказать, что площадь \(S_{KEMF}\) равна сумме площадей \(S_{BCE}\) и \(S_{AFD}\).

1. Запишем площадь \(S_{KEMF}\) через разность площадей:
\(
S_{KEMF} = S_{ABM} — S_{KBC} + S_{BCE} — S_{AKD} + S_{AFD}.
\)

2. Выразим площади треугольников через основание и высоту. Используем высоты \(h_1\), \(h_2\), \(h_3\), которые соответствуют треугольникам:
\(
S_{ABM} = \frac{1}{2}a \cdot h_2, \quad S_{KBC} = \frac{1}{2}a \cdot h_1, \quad S_{AKD} = \frac{1}{2}a \cdot h_3.
\)

Подставим:
\(
S_{KEMF} = \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot h_1 + S_{BCE} — \frac{1}{2}a \cdot h_3 + S_{AFD}.
\)

3. Найдем связь между высотами \(h_1\), \(h_2\), \(h_3\). Высота между сторонами \(AB\) и \(CD\) увеличивается линейно:
\(
h_2 — h_1 = h_3 — h_2 = d.
\)

4. Упростим выражение для \(S_{KEMF}\):
\(
S_{KEMF} = \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot (h_2 — d) + S_{BCE} — \frac{1}{2}a \cdot (h_2 + d) + S_{AFD}.
\)

Раскроем скобки:
\(
S_{KEMF} = \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot h_2 + \frac{1}{2}a \cdot d + S_{BCE} — \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot d + S_{AFD}.
\)

Сократим одинаковые члены:
\(
S_{KEMF} = S_{BCE} + S_{AFD}.
\)

Таким образом, доказано, что площадь \(S_{KEMF}\) равна сумме площадей \(S_{BCE}\) и \(S_{AFD}\).

Рассмотрим выпуклый четырехугольник \(ABCD\), где точки \(K\), \(E\), \(M\), \(F\) делят стороны \(AB\), \(BC\), \(CD\), \(DA\) на равные части. Пусть \(AK = KB = a\), \(CM = MD = b\). Требуется доказать, что площадь \(S_{KEMF}\) равна сумме площадей \(S_{BCE}\) и \(S_{AFD}\).

1. Запишем площадь \(S_{KEMF}\) через разность площадей:
\(
S_{KEMF} = S_{ABM} — S_{KBC} + S_{BCE} — S_{AKD} + S_{AFD}.
\)

2. Выразим площади треугольников через основание и высоту. Используем высоты \(h_1\), \(h_2\), \(h_3\), которые соответствуют треугольникам:
\(
S_{ABM} = \frac{1}{2}a \cdot h_2, \quad S_{KBC} = \frac{1}{2}a \cdot h_1, \quad S_{AKD} = \frac{1}{2}a \cdot h_3.
\)

Подставим площади треугольников в выражение для \(S_{KEMF}\):
\(
S_{KEMF} = \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot h_1 + S_{BCE} — \frac{1}{2}a \cdot h_3 + S_{AFD}.
\)

3. Найдем связь между высотами \(h_1\), \(h_2\), \(h_3\). Высота между сторонами \(AB\) и \(CD\) увеличивается линейно, что дает равенство:
\(
h_2 — h_1 = h_3 — h_2 = d.
\)

Отсюда:
\(
h_1 = h_2 — d, \quad h_3 = h_2 + d.
\)

4. Подставим значения высот \(h_1\) и \(h_3\) в выражение для \(S_{KEMF}\):
\(
S_{KEMF} = \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot (h_2 — d) + S_{BCE} — \frac{1}{2}a \cdot (h_2 + d) + S_{AFD}.
\)

Раскроем скобки:
\(
S_{KEMF} = \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot h_2 + \frac{1}{2}a \cdot d + S_{BCE} — \frac{1}{2}a \cdot h_2 — \frac{1}{2}a \cdot d + S_{AFD}.
\)

5. Упростим выражение, сократив одинаковые члены:
\(
S_{KEMF} = S_{BCE} + S_{AFD}.
\)

Таким образом, доказано, что площадь \(S_{KEMF}\) равна сумме площадей \(S_{BCE}\) и \(S_{AFD}\).