Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 836 Атанасян — Подробные Ответы
Прямая, проходящая через середины диагоналей \( AC \) и \( BD \) четырёхугольника \( ABCD \), пересекает стороны \( AB \) и \( CD \) в точках \( M \) и \( K \). Докажите, что площади треугольников \( DCM \) и \( AKB \) равны.
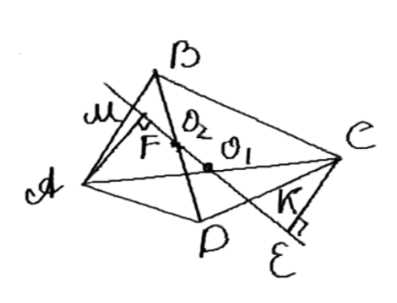
Рассмотрим четырехугольник \(ABCD\), где \(E \in AC\), \(F \in BD\), \(M = EF \cap AB\), \(K = EF \cap CD\). Требуется доказать, что \(S_{DCM} = S_{AKB}\).
1. Так как \(AE = EC\), высоты треугольников \(AMK\) и \(CMK\) равны (\(h_{AMK} = h_{CMK}\)). Следовательно, площади треугольников \(S_{AMK}\) и \(S_{CMK}\) равны:
\(
S_{AMK} = S_{CMK}.
\)
2. Так как \(BF = FD\), высоты треугольников \(BMK\) и \(DMK\) равны (\(h_{BMK} = h_{DMK}\)). Следовательно, площади треугольников \(S_{BMK}\) и \(S_{DMK}\) равны:
\(
S_{BMK} = S_{DMK}.
\)
3. Сложим равенства из пунктов 1 и 2:
\(
S_{AMK} + S_{BMK} = S_{CMK} + S_{DMK}.
\)
4. Площадь треугольника \(AKB\) равна сумме площадей \(S_{AMK} + S_{BMK}\), а площадь треугольника \(DCM\) равна сумме \(S_{CMK} + S_{DMK}\). Таким образом:
\(
S_{AKB} = S_{DCM}.
\)
Доказательство завершено.
Рассмотрим четырехугольник \(ABCD\), где точки \(E\) и \(F\) лежат на диагоналях \(AC\) и \(BD\) соответственно. Точки \(M\) и \(K\) являются пересечениями прямой \(EF\) с сторонами \(AB\) и \(CD\). Требуется доказать, что площади треугольников \(S_{DCM}\) и \(S_{AKB}\) равны.
1. Введем обозначения:
— \(AE = EC\), то есть точка \(E\) делит диагональ \(AC\) на две равные части.
— \(BF = FD\), то есть точка \(F\) делит диагональ \(BD\) на две равные части.
— \(M = EF \cap AB\), \(K = EF \cap CD\).
2. Рассмотрим треугольники \(AMK\) и \(CMK\). Так как \(AE = EC\), высоты этих треугольников, проведенные из вершины \(M\) к основанию \(AK\) и \(CK\), равны (\(h_{AMK} = h_{CMK}\)). Основания \(AK\) и \(CK\) также равны, так как \(E\) является серединой диагонали \(AC\). Следовательно, площади треугольников \(S_{AMK}\) и \(S_{CMK}\) равны:
\(
S_{AMK} = S_{CMK}.
\)
3. Аналогично рассмотрим треугольники \(BMK\) и \(DMK\). Так как \(BF = FD\), высоты этих треугольников, проведенные из вершины \(M\) к основанию \(BK\) и \(DK\), равны (\(h_{BMK} = h_{DMK}\)). Основания \(BK\) и \(DK\) также равны, так как \(F\) является серединой диагонали \(BD\). Следовательно, площади треугольников \(S_{BMK}\) и \(S_{DMK}\) равны:
\(
S_{BMK} = S_{DMK}.
\)
4. Сложим равенства из пунктов 2 и 3:
\(
S_{AMK} + S_{BMK} = S_{CMK} + S_{DMK}.
\)
5. Площадь треугольника \(AKB\) равна сумме площадей \(S_{AMK} + S_{BMK}\), а площадь треугольника \(DCM\) равна сумме \(S_{CMK} + S_{DMK}\). Таким образом:
\(
S_{AKB} = S_{DCM}.
\)
Доказательство завершено.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.