
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 827 Атанасян — Подробные Ответы
Постройте равнобедренную трапецию по основаниям и диагонали.
Дано: \( P_1Q_1, P_2Q_2, P_3Q_3 \) — отрезки. Требуется построить равнобедренную трапецию \( ABCD \) с основаниями \( AD \) и \( BC \), такими что \( AD = P_1Q_1 \), \( BC = P_2Q_2 \), \( AC = BD = P_3Q_3 \).
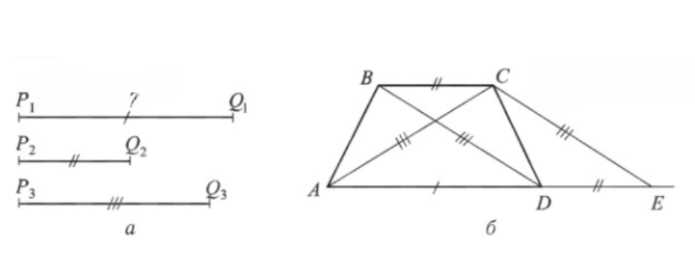
Пусть \( ABCD \) — искомая трапеция. На прямой \( AD \) откладываем отрезок \( DE \), равный \( BC \), так как \( DE = BC \) и \( DE \parallel BC \), то \( DECB \) — параллелограмм, а значит \( CE = BD = P_3Q_3 \).
В треугольнике \( \triangle ACE \): \( AC = CE = P_3Q_3 \), \( AE = AD + DE = P_1Q_1 + P_2Q_2 \).
Построение: строим \( \triangle ACE \), где \( AC = CE = P_3Q_3 \), \( AE = P_1Q_1 + P_2Q_2 \). На стороне \( AE \) отмечаем точку \( D \), такую что \( AD = P_1Q_1 \), и проводим через точку \( D \) прямую, параллельную \( CE \), а через точку \( C \) — прямую, параллельную \( AE \). Эти прямые пересекаются в точке \( B \).
Доказательство: по построению \( AD = P_1Q_1 \), \( DE = P_2Q_2 \), \( AC = P_3Q_3 \). Так как \( BC \parallel DE \) и \( BD \parallel CE \), то \( DECB \) — параллелограмм, а значит \( BC = DE = P_2Q_2 \), \( CE = BD = P_3Q_3 \). Таким образом, трапеция \( ABCD \) удовлетворяет всем условиям задачи.
Дано: \( P_1Q_1, P_2Q_2, P_3Q_3 \) — отрезки. Требуется построить равнобедренную трапецию \( ABCD \) с основаниями \( AD \) и \( BC \), такими что \( AD = P_1Q_1 \), \( BC = P_2Q_2 \), \( AC = BD = P_3Q_3 \).
Рассмотрим построение и доказательство задачи.
1. Пусть \( ABCD \) — искомая трапеция. На прямой \( AD \) откладываем отрезок \( DE \), равный \( BC \). Так как \( DE = BC \) и \( DE \parallel BC \), то \( DECB \) — параллелограмм. Следовательно, \( CE = BD = P_3Q_3 \).
2. Рассмотрим треугольник \( \triangle ACE \). У него выполнены следующие условия:
\( AC = CE = P_3Q_3 \), а также \( AE = AD + DE = P_1Q_1 + P_2Q_2 \).
3. Построение трапеции:
— Строим \( \triangle ACE \), стороны которого выражаются формулами:
\( AC = CE = P_3Q_3 \), \( AE = P_1Q_1 + P_2Q_2 \).
— На стороне \( AE \) отмечаем точку \( D \) так, что \( AD = P_1Q_1 \).
— Через точку \( D \) проводим прямую, параллельную \( CE \).
— Через точку \( C \) проводим прямую, параллельную \( AE \).
— Эти прямые пересекаются в некоторой точке \( B \).
4. Доказательство правильности построения:
— По построению \( AD = P_1Q_1 \), \( DE = P_2Q_2 \), \( AC = P_3Q_3 \).
— Так как \( BC \parallel DE \) и \( BD \parallel CE \) (по построению), то \( DECB \) — параллелограмм. Следовательно, \( BC = DE = P_2Q_2 \), \( CE = BD = P_3Q_3 \).
— Таким образом, трапеция \( ABCD \) удовлетворяет всем условиям задачи.
Ответ: трапеция \( ABCD \) построена, и её стороны удовлетворяют заданным условиям:
\( AD = P_1Q_1 \), \( BC = P_2Q_2 \), \( AC = BD = P_3Q_3 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!