ГДЗ по Геометрии 9 класс Номер 810 Атанасян — Подробные Ответы

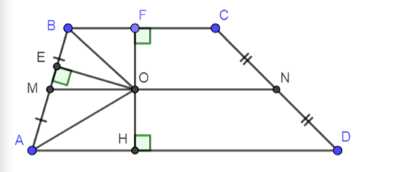
Докажите, что вершина угла, образованного биссектрисами двух углов трапеции, прилежащих к боковой стороне, лежит на прямой, содержащей среднюю линию трапеции.

Дано: \(ABCD\) — трапеция; \(\angle MBO = \angle OBC\), \(\angle MAO = \angle OAD\); \(BO \perp OA = O\). \(MN\) — средняя линия. Требуется доказать: \(O \in MN\).

Решение:

1. По теореме о биссектрисе неразвернутого угла, любая точка биссектрисы равноудалена от её сторон. Следовательно:
\(
OF \perp BC, \, OF \perp AB, \, OH \perp AD.
\)

2. Точка \(O\) лежит на биссектрисе угла \(ABC\), поэтому:
\(
OF = EO.
\)

3. Точка \(O\) также лежит на биссектрисе угла \(BAD\), следовательно:
\(
EO = OH.
\)

4. Из пункта 2 имеем:
\(
OF = EO.
\)
Из пункта 3 имеем:
\(
EO = OH.
\)

Так как средняя линия трапеции равноудалена от её оснований, то:
\(
OF = OH.
\)

Следовательно, \(O \in MN\). Что и требовалось доказать.

Дано: \(ABCD\) — трапеция, \(\angle MBO = \angle OBC\), \(\angle MAO = \angle OAD\), \(BO \perp OA = O\). \(MN\) — средняя линия. Требуется доказать: \(O \in MN\).

Решение:

1. Рассмотрим свойства биссектрисы угла. По теореме о биссектрисе неразвернутого угла, любая точка, лежащая на биссектрисе, равноудалена от её сторон. Это означает, что расстояния от точки \(O\) до сторон углов равны. Для угла \(ABC\) это расстояния \(OF\) и \(EO\), а для угла \(BAD\) это расстояния \(EO\) и \(OH\). Следовательно:
\(
OF = EO \quad \text{и} \quad EO = OH.
\)

2. Докажем, что точка \(O\) равноудалена от оснований трапеции \(AB\) и \(CD\). Из пункта 1 следует, что:
\(
OF = OH.
\)

3. Средняя линия \(MN\) трапеции определяется как геометрическое место точек, равноудалённых от оснований трапеции. Поскольку \(O\) равноудалена от оснований \(AB\) и \(CD\), то точка \(O\) принадлежит средней линии \(MN\).

4. Распишем это подробно:
а) Точка \(O\) лежит на биссектрисе угла \(ABC\), поэтому по свойству биссектрисы:
\(
OF = EO.
\)
б) Точка \(O\) также лежит на биссектрисе угла \(BAD\), следовательно:
\(
EO = OH.
\)
в) Из равенств \(OF = EO\) и \(EO = OH\) следует, что:
\(
OF = OH.
\)

5. Так как средняя линия \(MN\) трапеции равноудалена от её оснований \(AB\) и \(CD\), а точка \(O\) удовлетворяет этому условию (\(OF = OH\)), то:
\(
O \in MN.
\)

Ответ: доказано, что точка \(O\) лежит на средней линии \(MN\).