
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 790 Атанасян — Подробные Ответы
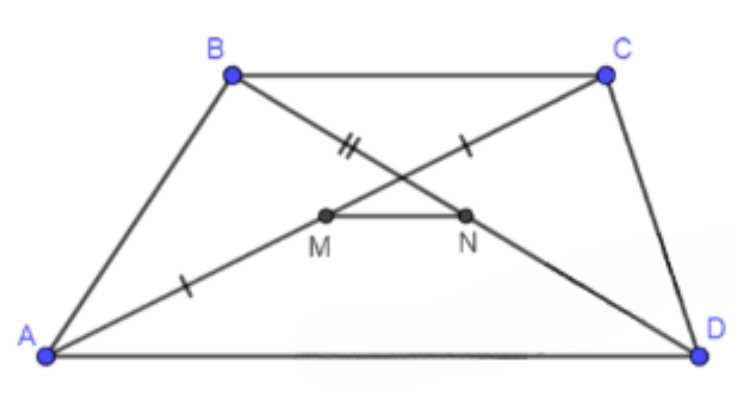
Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен полуразности оснований.
Дано: \(ABCD\) — трапеция; \(AC\), \(BD\) — диагонали; \(AM = MC\), \(BN = ND\).
Доказать: \(MN = \frac{1}{2}(AD — BC)\).
Решение:
По правилу многоугольника:
\(
MN = \overrightarrow{MA} + \overrightarrow{AD} + \overrightarrow{DN},
\)
\(
MN = \overrightarrow{MC} + \overrightarrow{CB} + \overrightarrow{BN}.
\)
Складываем равенства:
\(
2MN = \overrightarrow{MA} + \overrightarrow{MC} + \overrightarrow{DN} + \overrightarrow{BN} + \overrightarrow{AD} + \overrightarrow{CB}.
\)
Так как \( \overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{0} \), \( \overrightarrow{DN} + \overrightarrow{BN} = \overrightarrow{0} \), то:
\(
2MN = \overrightarrow{AD} + \overrightarrow{CB}.
\)
Получаем:
\(
MN = \frac{\overrightarrow{AD} + \overrightarrow{CB}}{2}.
\)
Так как \(AD \parallel BC\), то:
\(
MN = \frac{1}{2}(AD — BC).
\)
Ответ: \(MN = \frac{1}{2}(AD — BC)\).
Дано: \(ABCD\) — трапеция, \(AC\) и \(BD\) — диагонали, \(AM = MC\), \(BN = ND\).
Доказать: \(MN = \frac{1}{2}(AD — BC)\).
Рассмотрим трапецию \(ABCD\), в которой \(AD\) и \(BC\) — основания, а \(MN\) — отрезок, соединяющий середины диагоналей \(AC\) и \(BD\).
1) По правилу многоугольника:
\(
MN = \overrightarrow{MA} + \overrightarrow{AD} + \overrightarrow{DN},
\)
\(
MN = \overrightarrow{MC} + \overrightarrow{CB} + \overrightarrow{BN}.
\)
2) Складываем два равенства:
\(
2MN = (\overrightarrow{MA} + \overrightarrow{MC}) + (\overrightarrow{DN} + \overrightarrow{BN}) + (\overrightarrow{AD} + \overrightarrow{CB}).
\)
Так как \(AM = MC\) и \(BN = ND\), то \( \overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{0} \), \( \overrightarrow{DN} + \overrightarrow{BN} = \overrightarrow{0} \).
Тогда:
\(
2MN = \overrightarrow{AD} + \overrightarrow{CB}.
\)
3) Выразим \(MN\):
\(
MN = \frac{\overrightarrow{AD} + \overrightarrow{CB}}{2}.
\)
4) Поскольку \(AD \parallel BC\), их векторы направлены в противоположные стороны, поэтому модуль разности их длин равен разности модулей:
\(
|MN| = \frac{|AD — BC|}{2}.
\)
Таким образом, \(MN\) равно половине разности оснований трапеции:
\(
MN = \frac{1}{2}(AD — BC).
\)
Ответ: \(MN = \frac{1}{2}(AD — BC)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!