ГДЗ по Геометрии 9 класс Номер 1310 Атанасян — Подробные Ответы

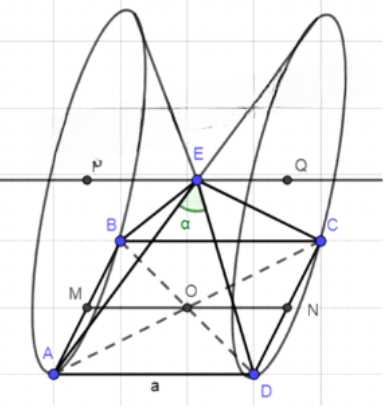
Правильная четырёхугольная пирамида со стороной основания a и плоским углом α при вершине вращается вокруг прямой, проходящей через вершину параллельно стороне основания. Найдите объём полученного тела.

1. Дано: \(FABC\) — правильная пирамида, \(AD = a\), \(S_{\triangle AED} = a^2\), \(PQ \parallel AD\).

2. Находим апофему \(EM\) из площади грани:
\(
\frac{1}{2}a \cdot EM = a^2 \quad \Rightarrow \quad EM = 2a
\)

3. Радиус конуса (высота пирамиды):
\(
r = \sqrt{(2a)^2 — \left(\frac{a}{2}\right)^2} = \frac{a\sqrt{15}}{2}
\)

4. Объем цилиндра (\(R = 2a\), \(H = a\)):
\(
V_{\text{цил}} = \pi (2a)^2 \cdot a = 4\pi a^3
\)

5. Объем двух конусов (\(h = \frac{a}{2}\)):
\(
2V_{\text{кон}} = 2 \cdot \frac{1}{3}\pi \left(\frac{a\sqrt{15}}{2}\right)^2 \cdot \frac{a}{2} = \frac{5\pi a^3}{4}
\)

6. Итоговый объем:
\(
V = 4\pi a^3 — \frac{5\pi a^3}{4} = \frac{11\pi a^3}{4}
\)

Ответ:
\(
\frac{11\pi a^3}{4}
\)

Дано: \(FABC\) — правильная пирамида, \(AD = a\), площадь боковой грани \(S_{\triangle AED} = a^2\), точка \(E \in PQ\), \(PQ \parallel AD\). Найти объем тела вращения.

Решение начинается с анализа геометрической конфигурации. Тело вращения образуется при вращении заданной фигуры вокруг оси и состоит из цилиндра с параметрами \(R = EM = 2a\) и \(H = a\), из которого удалены два одинаковых конуса с характеристиками \(r = PM = \frac{a\sqrt{15}}{2}\) и \(h = \frac{a}{2}\).

Ключевой шаг — определение апофемы пирамиды \(EM\) из условия площади боковой грани: \(\frac{1}{2} \cdot a \cdot EM = a^2 \Rightarrow EM = 2a\). Далее через прямоугольный треугольник \(EMO\) находится высота пирамиды \(PM = \sqrt{(2a)^2 — (\frac{a}{2})^2} = \frac{a\sqrt{15}}{2}\), которая одновременно является радиусом основания конусов.

Для объемных вычислений сначала определяется объем цилиндра: \(V_{\text{цил}} = \pi (2a)^2 \cdot a = 4\pi a^3\). Затем рассчитывается объем одного конуса: \(V_{\text{кон}} = \frac{1}{3} \pi (\frac{a\sqrt{15}}{2})^2 \cdot \frac{a}{2} = \frac{5\pi a^3}{8}\), а для двух конусов: \(2V_{\text{кон}} = \frac{5\pi a^3}{4}\).

Финальный объем тела вращения получается вычитанием: \(V = 4\pi a^3 — \frac{5\pi a^3}{4} = \frac{11\pi a^3}{4}\). Ответ: \(\frac{11\pi a^3}{4}\).